来自某教师群的一道三元不等式陈题改编

kuing

广东汕头达濠华侨中学李京会(39584****)  23:45:42

这道题显然改编自下面这道陈题（2003国家队培训题）



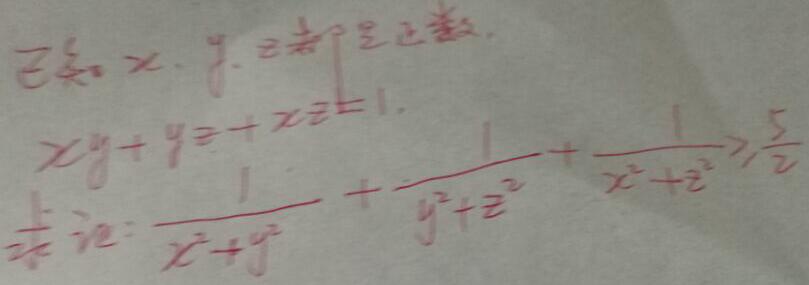
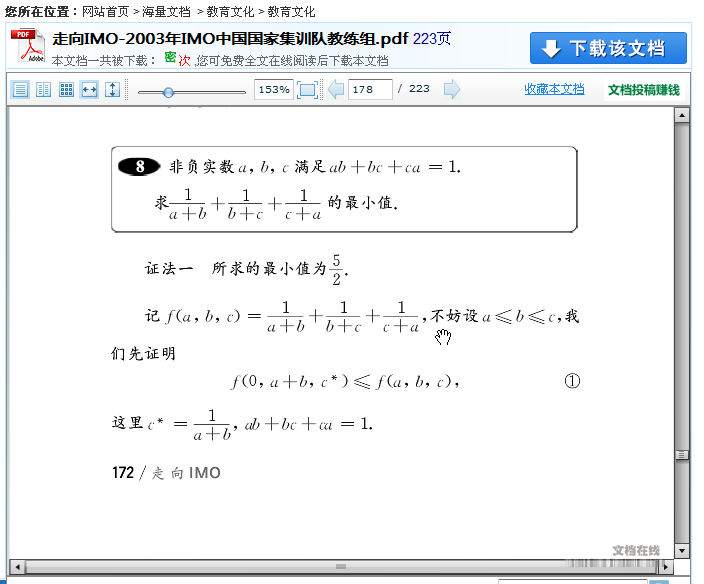
而其实又弱于这道陈题，根据陈题的结果，我们有如下不等式成立
\[\sum\frac1{a+b}\geqslant \frac52\cdot\frac1{\sqrt{ab+bc+ca}},\]
令 $a=x^2$, $b=y^2$, $c=z^2$ 得
\[\sum\frac1{x^2+y^2}\geqslant \frac52\cdot\frac1{\sqrt{x^2y^2+y^2z^2+z^2x^2}}
\geqslant \frac52\cdot\frac1{xy+yz+zx},\]
即得证。