$a<c,b<c,a^2+b^2>c^2$，问三角形形状

isee

在三角形$\triangle ABC$中，若$c$为最大边，且$a^2+b^2>c^2$,则此三角的形状是___?

不论方法，向大家讨教除余弦定理的解法。

kuing

那就用正弦呗
\[\sin^2A>\sin^2C-\sin^2B=\sin(C-B)\sin(C+B)=\sin(C-B)\sin A
\riff \sin A>\sin (C-B),\]

isee

回复 2# kuing


   

    这是自然这是自然。

isee

这个问题其实困惑我好几年了，基本所有资料上要么是余弦（或实为余弦定理）定理说之，或是直接给出结论。

我一度觉得肯定会有一个极为简洁的平几证明，所以都只给结论，而偶不知而已。

realnumber

勾股定理可以得出的,以a,b为直角边构造直角三角形，由图形可以得到C比直角小，又C>B,C>A,
这样算不算？

乌贼

如图，以$ AB $为直径作园，在园上取一点$ D $（$ D,C $不在$ AB $同侧），使$ AC=AD=b $，连接$ CD $有\[ a^2+b^2>c^2=AD^2+BD^2=b^2+BD^2 \]即\[ BC=a>BD \]所以$\triangle BDC$中\[ \angle CDB>\angle BCD \]
$\triangle ACD$中\[\angle CDA=\angle DCA\]即\[90\du = \angle BDA>\angle BCA \]
$ \triangle ABC $中大边对应的大角小于$ 90\du  $，$ \triangle ABC $为锐角三角形。

游客

以A为圆心，AC为半径的作圆；以B为圆心，BC为半径的作圆；
两圆交点C在以AB为直径的圆外.

乌贼

回复 7# 游客
得排除在园内（需要证明）的可能。不过也简单

游客

回复 8# 乌贼


    三圆心共线,在三圆有共点的情况下,固定两圆,变化第三个圆,很直观.

isee

5#6#7#其实都是一个意思，反证亦可，不过，都不算简单。
这都得承认一个事实 圆外角小于圆周角大小于圆内角。


我想仅就初中而言很可能就是从这个角度出发，而作为一个常用的结论，在竞赛书上。

isee

回复 2# kuing

"24 小时评分数超过限制"，不是我不给威望啊，，，，，

kuing

回复 11# isee

上次那帖我只是开玩笑啊威望什么的我根本不在乎……
况且上面我那只是水帖本来也不应该给威望……

isee

回复 12# kuing

快把这个设置再改改，24小时内多几个，也正常啊，有不同的主题帖嘛。。。。

kuing

回复 13# isee

懒得去设置里找了……
少也挺好的，少才会精，这么久我好像才给过几次，非常精彩的才会给

isee

回复 14# kuing


    {:curse:}

isee

源自知乎提问

几年后，自己从图形上解决了，本质上还是余弦定理换成图了

题：三角形 $ABC$ 中满足 $a^2+b^2<c^2$，则 $\angle C$ 为钝角.



由 $a^2<a^2+b^2<c^2$ 知 $a<c$，同理 $b<c$ 即 $c$ 为最大边亦是 $\angle C$ 为最大角. 以点 $A$ 为圆心， $AB$ 为半径作 $\odot A.$

如图 1 所示边 $AC, {~}BC$ 延长线分别交 $\odot A$ 于 $E,F,G$ 三点， $BD$ 为直径.

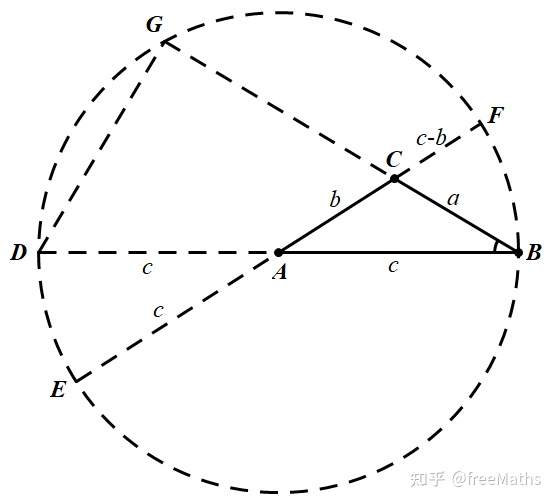
图 1 BD 为直径

由 $a^2+b^2<c^2$ 得 $(c-b)(c+b)>a^2$.

又易得 $\triangle FCB\sim \triangle GCE$，

有 $CF\cdot CE=CB\cdot CG$，

即 $(c-b)(c+b)=a\cdot CG>a^2$ 从而 $GC>a$.

进一步知 $a<GC=BG-a$，

所以 $a<\frac 12BG$ 这表明点 $A$ 在 $BG$ 上的投影——就是BG的中点——在 $BC$ 的延长线上，所以 $\angle ACB>90^\circ.$

也就是三角形是钝角三角形.

同样的可证若 $a^2+b^2>c^2$ 可得 $\angle C$ 为锐角.