已知$p,q,r$都是正数，求方程组的解

abababa

已知$p,q,r$都是正数，求下面方程组的解
\[p\sqrt{1-\frac{q(p+1)}{(p+q+1)^2}}=q\sqrt{1-\frac{r(q+1)}{(q+r+1)^2}}=r\sqrt{1-\frac{p(r+1)}{(r+p+1)^2}}\]
网友觉得只有$p=q=r$这种解，他想用不等式的方法证明没有其它解，但没得出结果。
已经得到的结论是：若任意两个数相等，例如$p=r$，则正数解只有$p=q=r$。

色k

看起来有点背景？

abababa

回复 2# 色k

我也不太清楚，网友发过来的，我用软件算了很长时间也没算出来，就把软件停了。

abababa

顶一下这帖。
后来我换了Maple软件算了一下，到是确实证实了猜测，只有$p=q=r$这种实数解，但软件算的不知道背后是什么原理，看不到过程。

abababa

回复 2# 色k

果然是有背景的，就是那个求证正三角形的，昨天被网友解决了，一会把他的解法发上来再看看。

abababa

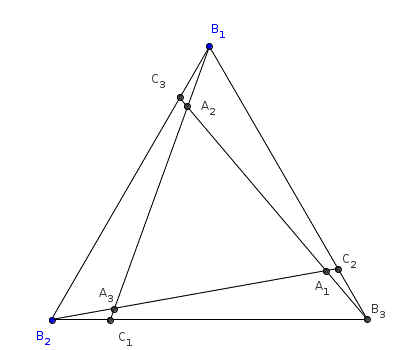
$\triangle A_1A_2A_3$是正三角形，$B_1C_3=B_2C_1=B_3C_2$，求证$\triangle B_1B_2B_3$是正三角形。
证明：
设$\triangle A_1A_2A_3$边长为$1$，设$(B_1A_2,B_2A_3,B_3A_1)=(p,q,r)$，设$\angle A_2B_1C_3=x$。

假设$x$是钝角，则$60^\circ < \angle A_1B_2C_3+60^\circ=\angle B_2C_3A_2=120^\circ-x < 30^\circ$矛盾，因此$x$是锐角。在$\triangle B_1B_2A_3$中，易知$B_1B_2^2=(p+1)^2+q^2+(p+1)q$，于是由$\frac{B_2A_3}{\sin x}=\frac{B_1B_2}{\sin 120^\circ}$得$\sin x=\frac{\frac{\sqrt{3}}{2}q}{B_1B_2}$，因此$\cos x=\frac{1}{2}\frac{2+2p+q}{\sqrt{(p+1)^2+q^2+(p+1)q}}$。在$\triangle B_1A_2C_3$中有$\frac{B_1A_2}{\sin(120^\circ-x)}=\frac{t}{\sin 60^\circ}$，因此$t=\frac{p\sqrt{(p+1)^2+q(p+1)+q^2}}{p+q+1}$。同理
\[t=\frac{p\sqrt{(p+1)^2+q(p+1)+q^2}}{p+q+1}=\frac{q\sqrt{(q+1)^2+r(q+1)+r^2}}{q+r+1}=\frac{r\sqrt{(r+1)^2+p(r+1)+p^2}}{r+p+1}\]
即
\[p^2(1-\frac{q(p+1)}{(p+q+1)^2})=q^2(1-\frac{r(q+1)}{(q+r+1)^2})=r^2(1-\frac{p(r+1)}{(r+p+1)^2})\]
令$f(x,y)=x^2(1-\frac{y(x+1)}{(x+y+1)^2})$，于是有$f(p,q)=f(q,r)=f(r,p)$。
易知当$x_1,x_2 > 0, x_1 \neq x_2$时有
\[\frac{f(x_2,x_1)-f(x_1,x_2)}{x_2-x_1} > 0 \tag{*}\]
当$x_1,x_2,\alpha > 0, x_1 \neq x_2$时有
\[\frac{f(x_2,\alpha)-f(x_1,\alpha)}{x_2-x_1} > 0 \tag{**}\]

若$p=q$或$q=r$或$r=p$，易知$p=q=r$。下面只讨论$p,q,r$两两不等的情况。假设$p < q$，由*知$f(q,p) > f(p,q)$，但已知$f(p,q)=f(r,p)$，于是$f(q,p) > f(r,p)$，再由**知$q > r$，因此由*知$f(q,r) > f(r,q)$，但已知$f(q,r)=f(p,q)$，于是$f(p,q) > f(r,q)$，再由**知$p > r$，因此由*知$f(p,r) > f(r,p)$，但已知$f(r,p)=f(q,r)$，于是$f(p,r) > f(q,r)$，再由**知$p > q$，这与假设$p < q$矛盾，因此假设错误，于是$p \ge q$。同理有$q \ge r, r \ge p$，于是$p \ge q \ge r \ge p$，因此$p=q=r$。于是有$\triangle B_1B_2A_3 \cong \triangle B_2B_3A_1 \cong \triangle B_3B_1A_2$，从而$\triangle B_1B_2B_3$是正三角形。

把网友QQ里的文本打成latex了，中间改了几个打字错误，我觉得总体上证明没问题。大家再看看有没有什么错误。

游客

abababa

回复 7# 游客

谢谢，但你说的“显然，随着$C_2A_1$的增加，锐角$\angle C_2B_3A_1$减小”，我觉得不够显然，如果从图上看，把$C_2$向右上方拉，这时角是增大的，当然因为有其它的限制它可能确实减小了，但这只是直观上的感觉，能不能用证明的方式证明一下？

游客

回复 8# abababa


    变化之前先确定B1的位置。

abababa

回复 9# 游客

我还是不怎么懂$C_2A_1$应该如何增加。能不能用代数的方法更明确一点，就是把固定的点写成确定的坐标，把$\angle C_2B_3A_1$随$C_2A_1$的增加关系写成确定的函数方式，这样看起来更明确，不然总觉得是根据图来说理，虽然直观但不够严谨。