|
|
Last edited by hejoseph 2016-12-7 11:00边长已知道且有外接圆的自交五边形比凸五边形复杂得多,只要边长已知,凸五边形必定是全等的,但自交五边形却不一定,例如下面两个五角星
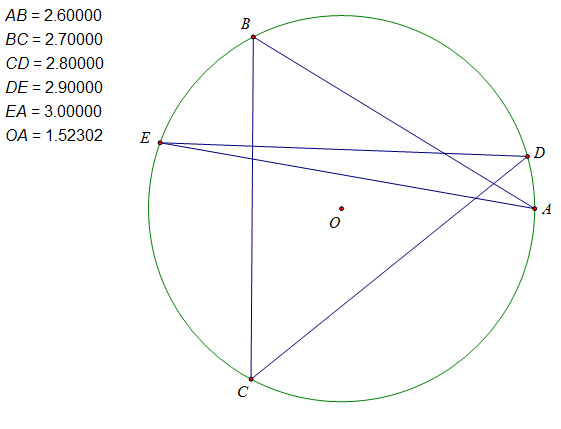
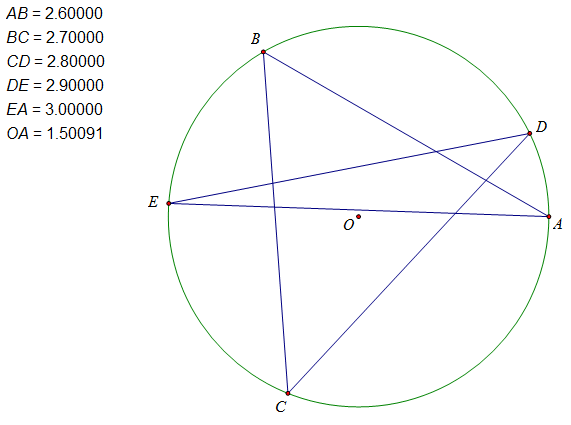
另外,自交五边形的半径大小也很难看出有什么规律。
五边形边长按顺序是 $a,b,c,d,e$,外接圆半径是 $R$,这里五边形包括自交五边形,这些五边形的半径都满足同一个关于 $R^2$ 的七次方程(系数都是 $a,b,c,d,e$ 的多项式),这里的问题是:证明凸五边形外接圆的半径一定是这个方程的最大正根。
这个凸五边形的结论应该对任意边长已知且有外接圆的凸多边形都成立。 |
|