，求顶点C的轨迹方程。

天音

已知常数$a>b>0$，点$A(-a,0)$是直角三角形ABC的直角顶点，顶点B在直线$x=b$上移动，斜边BC所在直线恒过点$D(a,0)$，求顶点C的轨迹方程。

kuing

这没啥难的吧，至少代数方法毫无难度。

踏歌而来

回复 1# 天音


给个思路。
设C（x0，y0），可得出CD的方程。
然后，令x=b，可得出B点坐标。
然后Kab*Kbc=-1
即可得到：
xo、y0、a、b的二元二次方程：

然后把x0、y0换成x、y即可。

kuing

或者酱：

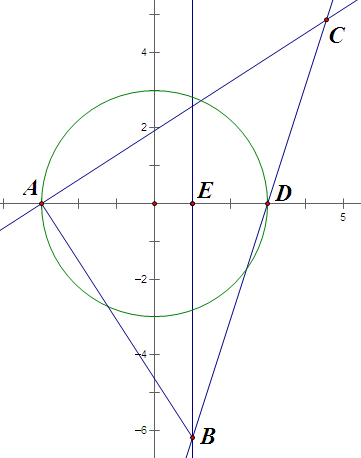
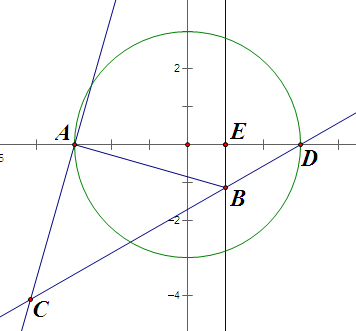
无论哪种情况，都有
\[k_{AC}\cdot k_{DC}=\cot \angle BAE\cdot \tan \angle BDE=\frac{AE}{BE}\cdot \frac{BE}{DE}=\frac{AE}{DE}=\frac{a+b}{a-b},\]
所以轨迹为
\[\frac{x^2}{a^2}-\frac{y^2}{a^2\frac{a+b}{a-b}}=1.\]

值得一提的是，其实 $b$ 也可以大于 $a$，同样也会有 $k_{AC}\cdot k_{DC}=(a+b)/(a-b)$，所以方程也是一样的。