高三一个函数题$f(x)=\ln x-ax^2-2x$

realnumber

$f(x)=\ln x-ax^2-2x$
1.若f(x)在$x\in (0.25,2)$单调递减，求a的取值范围.
2.当a=-0.25时，关于x的方程$f(x)=-0.5x+b$在[1,4]上恰有2个不等的实数根，求实数b的取值范围.

realnumber

1.由题意$f'(x)=\frac{1}{x}-2ax-2\le 0$,
即$\frac{1}{x^2}-\frac{2}{x}\le 2a$
看来换下元就解决问题了$t=\frac{1}{x} \in $[0.5,4]
只需要$(t^2-2t)_{max}\le 2a$,即$4\le a$.
2.
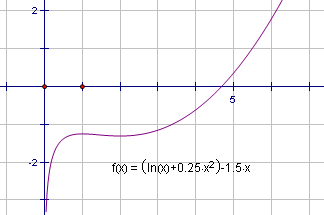
问题等价于$b=\ln{x}+\frac{1}{4}x^2-\frac{3}{2}x,x\in$[1,4]有2解，
构造函数$f(x)=\ln{x}+\frac{1}{4}x^2-\frac{3}{2}x$如图.
求导，考察单调性，配合图，可得出$f(2)< b\le f(1)$.
因为是某学生作业，具体过程没写.