一道貌似简单的圆的问题

敬畏数学

A(0，1),B(2，0),圆C的圆心为（5,6），半径为r，线段AB上任意一点P，M,N为圆C上两点，若M为PN的中点，求圆C的半径r的范围。
此题能否直接用几何解决？请教高手。那些代数方法已经OK。谢谢坛子里的高手。。。。

色k

当 $\odot C$ 和 $M$ 固定时，作动点 $N$ 关于 $M$ 的对称点 $N'$，则显然 $N'$ 的轨迹就是与 $\odot C$ 关于 $M$ 对称的圆（除 $M$ 外），如左图所示。

　　　　

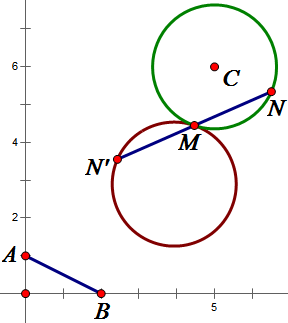
让 $M$ 在 $\odot C$ 上动运，则 $N'$ 的轨迹将扫出一个圆环区域，如右图所示。记此区域为 $\Omega$，具体写出来就是 $\Omega=\{(x,y)\mid r^2<(x-5)^2+(y-6)^2\leqslant (3r)^2\}$。

那么，满足题设当且仅当 $\Omega$ 与线段 $AB$ 有公共点。

由于恰好 $AB\perp BC$，所以由图形可知，$r$ 最小时就是 $\Omega$ 与 $AB$ 切于点 $B$ 时，即 $r_{\min}=BC/3$，而上确界就是当 $r\to AC$ 时，所以 $r$ 的范围是 $\bigl[\sqrt5,5\sqrt2\bigr)$。