一个高三翻折问题

realnumber

在等腰直角 $\triangle A B C$ 中，$A B \perp A C, B C=2, M$ 为 $B C$ 中点，$N$ 为 $A C$ 中点，$D$ 为 $B C$ 边上一个动点，$\triangle A B D$ 沿 $A D$ 翻折使 $B D \perp D C$，点 $A$ 在面 $B C D$ 上的投影为点 $O$，当点 $D$ 在 $B C$ 上运动时，以下说法错误的是（ ）

A．线段 NO 为定长
B．$|C O| \in[1, \sqrt{2})$
C．$\angle A M O+\angle A D B>180^{\circ}$
D．点 $O$ 的轨迹是圆弧

kuing

解决也有很多种的。

若是应试式地做出答案是 easy 的，因为存在快速发现选 C 的路子：
显然 $\angle AMO$ 必为锐角，故当 $D$ 在 $M$ 的右边时，那两个角都是锐角，所以 C 错。

若是大概地正面解答这题，也不难：
因 $O$ 是 $A$ 的投影点，$M$ 在平面上，故 $AO\perp OM$，
因 $MC\perp AO$, $MC\perp MA$，故 $MC\perp\Rtt AMO$，
由这两点可见 $O$ 恒在一个圆上，该圆以 $AM$ 为直径，且垂直于平面 $ABC$。
这样，A、B、D 看起来都是正确的。

而如果要真正严格的做这道，还要做一件有点麻烦的事，那就是说明轨迹的完整性。
事实上目前只能肯定 A 正确，B、D 还不能肯定，因为目前只是得出 $O$ 在圆上，有没有范围还不知道。

怎么说明好呢？晚点再说，先看会片。

kuing

续：
设翻折后的 $B$ 为 $B'$，设二面角 $B'$-$CD$-$A$ 的大小为 $\theta$，显然轨迹的完整性取决于 $\theta$ 能取到哪些值。



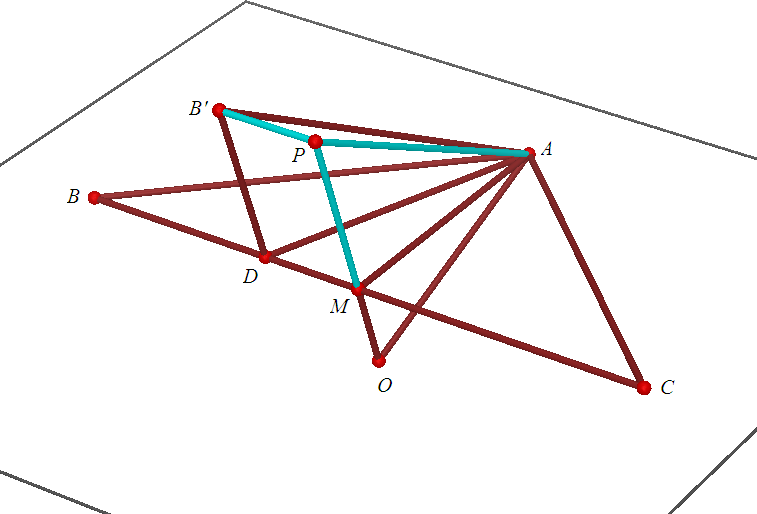
作如图所示的辅助线，设 $BD=x\in(0,2)$，则 $PM=x$, $AM=1$, $AP^2=B'A^2-B'P^2=2-(x-1)^2$，所以
\[\cos\theta=\frac{x^2+1-2+(x-1)^2}{2x}=x-1\in(-1,1),\]
也就是说 $\theta$ 能取遍 $(0,\pi)$，可见 $O$ 的轨迹是那个圆但要挖去 $A$ 点。

这样就可以肯定 B 是正确的，但 D 呢？挖掉一个点的圆算不算“圆弧”？我还真不清楚喔，你们说哩？

注：$\cos\theta=x-1$ 这结果如此简洁，看来会有更简单的证法，煮饭先……

kuing

再续：
嗯，用三面角余弦定理即可，即
\[\cos \angle ADB'=\sin \angle ADC\sin \angle B'DC\cos \theta +\cos \angle ADC\cos \angle B'DC,\]
所以
\[\cos \angle ADB=\sin \angle ADB\cos \theta \riff \cos \theta =\cot \angle ADB=x-1.\]

如果没搞错的话，一般的翻折有
\[\cos \theta =\cot \frac{\angle B'DC}2 \cot \angle ADB.\]

乌贼

$ AO\perp MO,AO\perp BC $所以$ AO\perp B_1DC $有$ O $为点$ A $在平面$ B_1DC $上的投影

游客