请教一个题目，向量几何最值

joatbmon

不会做，请教大家

joatbmon

图片显示有点难看，我手打题目
半径为1的扇形$AOB$中，$\angle AOB=60^\circ,P$为弧上动点，$AP$与$OB$延长线交于点$C,$则$\vv{OP}\cdot\vv{PC}$的取值范围为

kuing

呃，你原题那字母上面的箭头都看不到，只看到一条横线，理应当作是有向线段啊

kuing

姆……要是真按向量玩的话，这题看来得扔啊，我已经看到了四次方程的影子……

kuing

唉，又是不知谁在随便命题坑人啊……



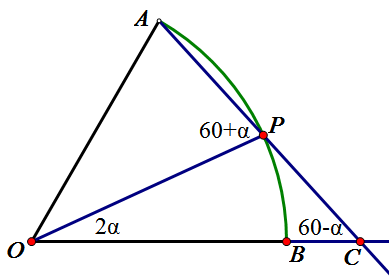
如图，得
\begin{align*}
\vv{OP}\cdot\vv{PC}&=PC\cos (60+\alpha ) \\
& =\frac{\sin 2\alpha \cos (60+\alpha )}{\sin (60-\alpha )} \\
& =\frac{\sin 2\alpha \cos (60+\alpha )}{\sin (60+\alpha )\cos 2\alpha -\cos (60+\alpha )\sin 2\alpha } \\
& =\frac1{\tan (60+\alpha )\cot 2\alpha -1}, \\
\end{align*}
令 $\tan \alpha =\sqrt3\cdot t$, $t\in (0,1/3)$，则
\[\tan (60+\alpha )\cot 2\alpha =\frac{\sqrt3(1+t)}{1-3t}\cdot \frac{1-3t^2}{2\sqrt3t}=\frac{(1+t)(1-3t^2)}{2t(1-3t)},\]
从而
\[\vv{OP}\cdot\vv{PC}=\frac1{\frac{(1+t)(1-3t^2)}{2t(1-3t)}-1}=\frac{2t(1-3t)}{(1-t)(1+3t^2)}=f(t),\]
要求它的最大值，求导计算最终得
\[f'(t)=0 \iff 9t^4-6t^3+6t-1=0,\]
四次方程来了，快逃！

joatbmon

多谢答复，朋友给的题，说找不到那本书的答案了。。。。