2017永康模拟（立体几何））

hjfmhh

kuing

图里有两个F是怎么回事啊，而且不但图，连题目也是，后面估计是 $\triangle CGH$ 沿 GH 折

乌贼

$CN^2=MN^2+AM^2$处，应该还有最小值

乌贼

回复 3# 乌贼
本想算一算，出现4次方，放弃……

kuing

把取值范围也算出来了。



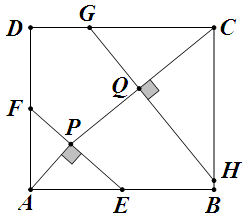
作 $AP\perp EF$ 于 $P$，连结 $PC$，则翻折后能让 $A$, $C$ 重合当且仅当 $GH\perp PC$ 并且它们的交点 $Q$ 满足 $AP^2+PQ^2=QC^2$。

依照这些设定，经过一系列的计算（过程懒得写出，反正也不好看，我是建系硬解的），最终可得
\[\led
CG&=\frac{x^4+2x^2+16}{2x^3+4x},\\
CH&=\frac{x^4+2x^2+16}{2x^2+16},
\endled\]
于是，要满足题意，当且仅当 $x$ 满足如下不等式组
\[\led
x&\geqslant \frac{x^4+2x^2+16}{2x^3+4x},\\
2&\geqslant \frac{x^4+2x^2+16}{2x^2+16},
\endled\]
解得
\[\sqrt{\sqrt{17}-1}\leqslant x\leqslant \sqrt{1+\sqrt{17}}.\]