杭二函数一题

hjfmhh

  选项A怎么排除

kuing

作 $f(x)$ 和 $e^{-x}+t$ 的图象如下。



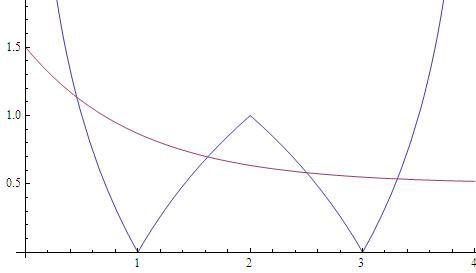
当 $t$ 趋向上界，即 $e^{-x}+t$ 上移至趋向过点 $(2,1)$ 时，$x_2\to2$，而 $x_1$ 显然并不趋向 $0$，所以此时必有 $x_1+x_2>2$，排除 A。

注意如果直线 $y=C$ 与 $y=f(x)$ 在 $0<x\leqslant2$ 这段有两交点，则易知它们的横坐标之积为 $1$，故此由图可知必有 $x_1x_2<1$（如果反应不过来，不妨画一条水平线穿过第二个交点），排除 B。

因为 $2<x_3<3<x_4<4$，故 $0<(x_3-4)(x_4-4)<2$（其实仿上还可以证明 $(x_3-4)(x_4-4)>1$ 呢），所以 D 成立。

但是 C 看起来似乎也是成立的？

hjfmhh

答案是C，选项A，D不好具体排除

走走看看

x1x2<1好证，x3x4<9证不出来。
请问如何证明x3x4<9呢？

hjfmhh

基本不等式

hjfmhh

A感觉错，但不好具体说明

kuing

回复 6# hjfmhh

我不是已经写了 A 的错因了么？

另外，D 是正确的啊

走走看看

回复 5# hjfmhh

还是做不出来，请做出来看看。

zhcosin

从 kk 那个图上可以“数形结合”出$0<x_1<1<x_2<2<x_3<3<x_4<4$，又有
\begin{align*}
-\log_2 x_1 & = e^{-x_1}+t \\
\log_2 x_2 & = e^{-x_2}+t \\
\log_2 (4-x_3) & = e^{-x_3}+t \\
-\log_2 (4-x_4) & = e^{-x_4}+t
\end{align*}
前两式相减得
\[ 0>e^{-x_2}-e^{-x_1}=\log_2 x_2 + \log_2 x_1 = \log_2 (x_1x_2) \]
得到 $x_1x_2<1$，选项B错误.

kuing

x1x2<1好证，x3x4<9证不出来。
请问如何证明x3x4<9呢？
走走看看 发表于 2017-6-1 10:27

事实上 $x_3+x_4<6$，看下面的图就知道，所以 $x_3x_4<9$。



当然了，看图不能代替证明，晚点再想想怎么写……

hjfmhh

1. (x3-4)(x4-4)>1
2. 15+x3x4>4(x3+x4)>8sqrt(x3x4)又2<x3<3<x4<4
3. 4<x3x4<9

Copy the Code

hjfmhh

回复 2# kuing


    2楼中的x1为什么显然不趋向于0

kuing

2楼中的x1为什么显然不趋向于0
hjfmhh 发表于 2017-6-1 22:50

假如 $x_1\to0$，则 $f(x_1)\to+\infty$，而 $e^{-x_1}+t$ 不可能无穷大，无可能相等。

走走看看

回复 11# hjfmhh

这样变形确实没想到，谢谢你！
也谢谢大家！

力工

这题应该是多选啊，C,D都对了。

敬畏数学

mark