一道几何证明题

TSC999

A 点在圆 O 上，AB 垂直于圆 O 的一条直径。以 A 为圆心，以 AB 为半径作另一圆交圆 O 于 D、C 两点。
连接 DC，与 AB 交于 E 点。求证 E 点将 AB 平分。

kuing

设 $OA$ 与 $CD$ 交于 $F$，则
\[AE=\frac{AF\cdot AO}{AB}=\frac{AC\cos \angle OAC\cdot AO}{AB}=AO\cos \angle OAC=\frac{AC}2=\frac{AB}2.\]

abababa

前几天刚做的这个。两边延长$AB$交下圆于$N$交上圆于$M$，然后$AE\cdot EN=CE\cdot DE=BE\cdot EM$，就是$AE(EB+BN)=EB(AE+AM)=EB(AE+AB)=EB(AE+BN)$，展开就得结果了。

色k

回复 3# abababa

这个证法有趣儿

TSC999

回复 2# kuing


    方法很简明，赞一个！

TSC999

回复 3# abababa



利用 DC 是两个圆的公共弦推出许多等式，这个证法确实很有趣！

乌贼

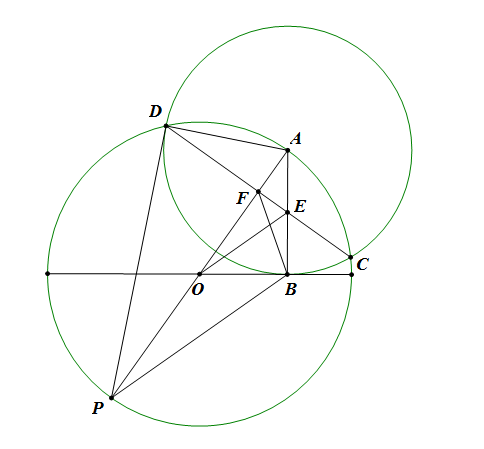
如图，延长$ AO $交园$ O $于点$ P $，设$ AO,CD $的交点为$ F $，连接$ AD,PD,BP,BF,OE $，有\[ \triangle ADF\sim \triangle DPA\riff \dfrac{AF}{AD}=\dfrac{AD}{AP}=\dfrac{AF}{AB}\riff \triangle ABP\sim \triangle AFB\riff \angle FBE=\angle APB \]又$ O,B,E,F $四点共圆有\[ \angle FBE=\angle FOE=\angle APB\riff OE\px PB\riff AE=EB \]

乌贼

这题中含一引理：$ CD $为圆$ O $与园$ O_1 $的公共弦，圆心$ O_1 $在园$ O $上，$ E $为$ CD $中点，$ O_1O $的延长线交园$ O $于$ Q $，$ P $为园$ O_1 $上任意点。则$ \angle O_1QP=\angle O_1PE $

乌贼

类似，来自几何吧之潘氏定理：
tieba.baidu.com/p/1403268127
已知：园$ O $是$ \triangle ABC $外接圆，$ BC $是直径，$ D $是圆弧$ BC $（线段$ BC $下方）上一点，$ DE\perp BC $于$ E $，$ DF\perp AB $于$ F $，$ EF $交$ AD $于$ G $。求证：$ G $是$ AD $中点。

乌贼

延长$ DE $交园$ O $于$ H $，有\[ DE=EH \]连接$ AH $，又$ B,D,E,F $四点共圆，有\[ \begin{align*}
&\angle DHA+\angle ABD=\angle DEF+\angle FBD=180\du\\&\angle DHA=\angle DEF \riff EF\px AH
\end{align*}\]即$ DG=GA $