|
|
Last edited by hbghlyj 2025-5-18 07:46初 251.(万喜人 徐伯儒编)已知 $\triangle \mathrm{ABC}, \mathrm{AB}>AC, \mathrm{AD}$ 是角平分线, EF 是 $\angle B A C$的外角平分线,点 $E 、 F$ 满足 $B E / / A D / / C F$ .作 $P Q / / B C$ 交 $A B 、 A C$ 分别于点 $P 、 Q$ ,直线 $E P$ 与 $F Q$ 交于点 $N$.点 $M$ 是 $B C$ 的中点.求证:$M N \px A D$ .
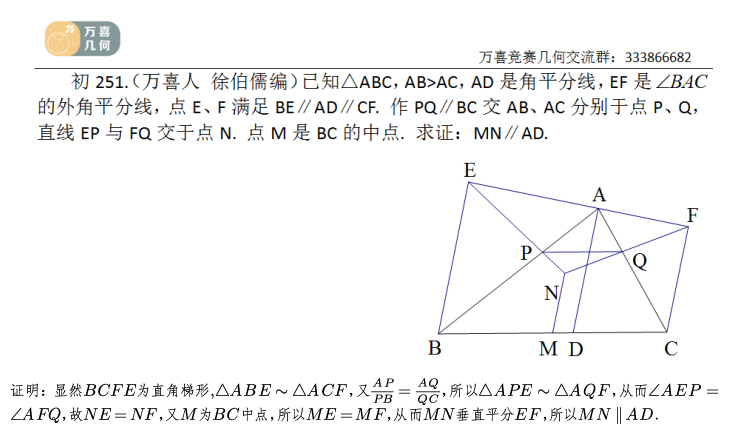
证明:显然 $B C F E$ 为直角梯形,$\triangle A B E \sim \triangle A C F$ ,又 $\frac{A P}{P B}=\frac{A Q}{Q C}$ ,所以 $\triangle A P E \sim \triangle A Q F$ ,从而 $\angle A E P=$ $\angle A F Q$ ,故 $N E=N F$ ,又 $M$ 为 $B C$ 中点,所以 $M E=M F$ ,从而 $M N$ 垂直平分 $E F$ ,所以 $M N \px A D$ . |
|