不用极点极线有没有简洁证明

乌贼 · 2017-6-23 02:11

Last edited by 乌贼 2017-6-23 11:54写完整，如图：$ FC $分别交$ MI $，园$ I $于$ G,F_1 $，$ MD $交$ IC $于$ Q $，$ EB $交园$ I $于$ E_1 $，主要分二步

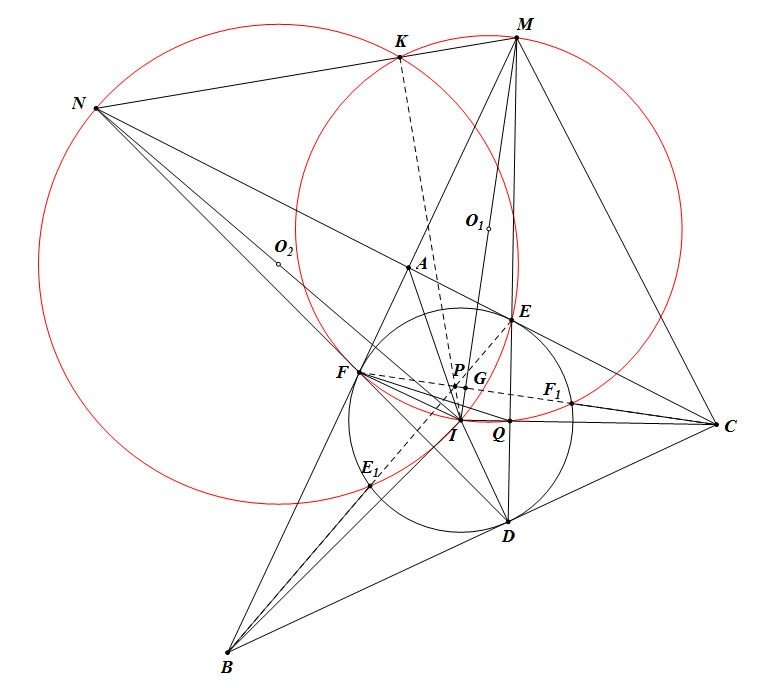
第一步：证明三园两两相交
由\[ \dfrac{FI}{IQ}=\dfrac{DI}{IQ}=\dfrac{IC}{DI}=\dfrac{IC}{FI}\riff \triangle FIQ\sim \triangle CIF \riff \angle IFQ=\angle FCI \]又\[ \angle IFQ=\angle IMQ \]所以$ M,G,Q,C $四点共圆，有\[ \angle MGC=\angle MQC=90\du \]即$ MI $垂直平分$ FF_1 $，故$ M,F,I,F_1 $四点共圆$ O_1 $。
同理：$ N,E,I,E_1 $四点共圆$ O_2 $。
作$ IK $垂直$ MN $于$ K $，有$ LK $为园$ O_1,O_2 $的公共弦，$ FF_1 $为园$ I,O_1 $的公共弦，$ EE_1 $为园$ I,O_2 $的公共弦。
第二步：证明$ K,P,I $三点共线。可由引理得，或另需证明，待续……

isee · 2017-6-23 23:01

回复 21# 乌贼

这个素材的确是丰富的。。。。。。

hbghlyj · 2021-5-3 22:31

条件如图, M为EF中点, 求证$OM^2=AO^2+EM^2$.

hbghlyj · 2021-5-3 22:42

BTW这帖5楼为什么最后S属于FeR可以推出两圆正交？(问完即删)

hbghlyj · 2023-1-9 06:10

zhcosin 发表于 2017-6-20 08:14
回复 3# kuing
TeXmacs 转出来的代码，我原来那里是个逗号，估计这个 \nocomma 是“非逗号"? ...

\nocomma 称为 Invisible Separator (也称为Invisible comma, Unicode码点U+2063).
此处用来分隔两个字母 (在TeXmac中,字母连着写就会变成直体)

TeXmacs manual 3.9. Semantics of mathematical symbols 右边是Table 3.5. Homoglyphs supported by TeXmacs. 在TeXmacs中输入逗号按两次Tab就得到Invisible Separator 或者输入\symbol按回车,再输入nocomma回车.
在TeXmacs中$\vv{AB}$如何输入?Have prettier arrows to write vectors? Copy as LaTeX结果为 \overrightarrow{A \nocomma B} Copy the Code

在formulas.tex可以找到

...
Start TeXmacs macros
\newcommand{\nocomma}{}
...
End TeXmacs
macros
\begin{document}
\begin{itemizedot}
\item $\mathbbm{I} \subset \mathbbm{N} \nocomma,
...

Copy the Code

在TeXmacs-2.1.2-src/TeXmacs/progs/convert/latex/latex-texmacs-drd.scm可以找到
;; other extra symbols
oempty exterior Exists bigintwl bigointwl
of suchthat barsuchthat asterisk point cdummy comma copyright
bignone nobracket nospace nocomma noplus nosymbol
dotminus dotpm dotmp dotamalg dottimes dotoplus dototimes dotast
into longminus longequal
longhookrightarrow longhookleftarrow
...

在 User preferences 取消勾选 Allow for macro definitions in preamble

见Cleaning up TeXmacs LaTeX export
见manual texmacs2latex

Certain TeXmacs macros like strong have no direct LaTeX analogues. For a certain number of frequently used macros, TeXmacs automatically generates macro definitions in the preamble of the LaTeX target file. This allows you to preserve as much structure as possible of your document, which is for instance useful if you import the document back into TeXmacs.

However, certain journals instruct authors to refrain from the definition of additional macros in the preamble. When disallowing for macro definitions in preambles, TeXmacs will automatically expand all corresponding macro applications.

Account		Remember me	Forgot password?
Password			Register account

[几何] 不用极点极线有没有简洁证明

不用极点极线有没有简洁证明呢{:shocked:}