2017北京解几是个什么梗？

力工

已知点$P(1,1)$，过点$(0,\dfrac{1}{2})$作直线$l$交抛物线$C:y^2=x$于不同的两点$M,N$，过点$M$作$x$轴的垂线分别 与直线$OP,ON$交于点$A,B$，求证：$A$为线段$BM$的中点.
几何角度怎么解答？

kuing

纯几何不知道，只知道这明显又是极点极线调和分割的那些东西搞粗来的。



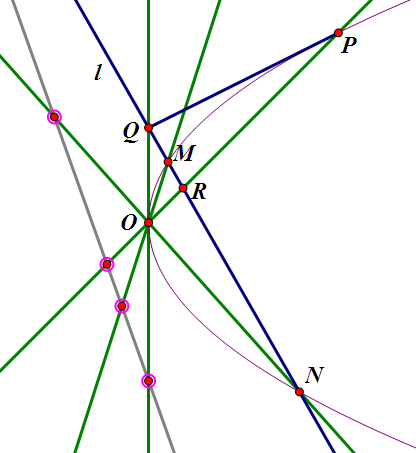
首先将点 $(0,1/2)$ 记为 $Q$，注意到 $QP$, $QO$ 都与抛物线相切，可见 $Q$ 的极线就是 $OP$。

设 $l$ 与 $OP$ 交于 $R$，则 $Q$, $M$, $R$, $N$ 为调和点列，那么 $OQ$, $OM$, $OR$, $ON$ 为调和线束（图中的绿线）。

于是，任意一条直线与这四条直线的交点亦为调和点列（比如图中左边的灰线交的四点）。

而现在是过 $M$ 作 $x$ 轴的垂线，是平行于 $OQ$ 的，即与 $OQ$ 的交点是无穷远点，那么剩下的三点就是中间的是中点了。

isee

回复 2# kuing


    嗯，这么一看，这就是本质。只不过顶楼用的解析方法（也是十分可行的方法）。


    补充一下2楼，纯几何就是完全四边形了（——本质都是射影几何）

   forum.php?mod=viewthread&tid=4175

   通常只要会链接中的顶楼和链接中的13楼（就是2楼的一部分前段，与后段）

色k

前几天才说过，用射影几何来玩往往能看清题目的本质以及将结论推广。

这年头以极点极线什么的为背景的解几题太多了，你们应该要了解下，至少一些基本性质要知道。

力工

射影几何连个身影有几何都不鸡道。。。