圆中证线段垂直

isee

设$A$、$B$是$\odot O$内部两点，且$O$为线段$AB$的中点，$P$是$\odot O$上一点，直线$PA$，$PB$与$\odot O$的另一交点分别为$C$、$D$.$\odot O$在$C$、$D$两点处的切线交于点$Q$，$M$为$PQ$的中点，求证：$OM \perp AB$.

kuing

瞬间想起《撸题集》第 856 页题目 6.5.13，不知有没有联系……

isee

回复 2# kuing


    还好还好，不是秒了，吓我跳，这题竞赛级别。

kuing

瞬间想起《撸题集》第 856 页题目 6.5.13，不知有没有联系……
kuing 发表于 2017-11-15 20:57

还真是可以互化的：

isee

回复 4# kuing


    ，我也想起来了，撸题集》第 856 页题目 6.5.13 是常见的，这个稍改了下。。。。。。。。。

乌贼

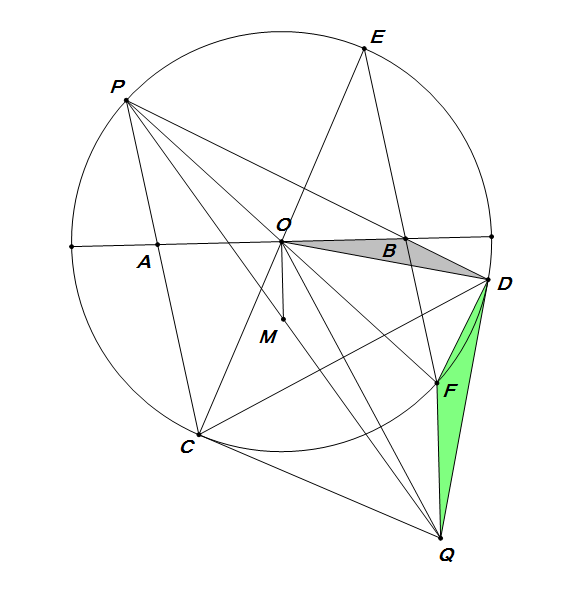
如图，连接$ CO $并延长交园$ O $于点$ E $，连接$ PO $并延长交园$ O $于点$ F $，连接$ EF $，由蝴蝶定理知$ EF $过$ B $点（或者直接证明$E,B,F$三点共线也容易）。
又$ O,C,Q,D $四点共圆\[ \angle OQD=\angle OCD=\angle BFD \]即\[ \triangle BDF\sim \triangle ODQ\riff \dfrac{BD}{OD}=\dfrac{DF}{DQ} \]加之\[ \angle BDQ=\angle DPF=\angle FDQ \]所以\[ \triangle BDO\sim \triangle FDQ\riff \angle FQD=\angle BOD \]因此$ QF\perp OB $（因为$ OD\perp DQ $）又\[ OM\px FQ\riff OM\perp AB \]