两道平几题

guanmo1

如题

kuing

圆的那道显然不需要搞出两个内切小圆来（命题者想吓人？），因为图形上下两部分完全独立，所以在其中一部分就必然会有结论。

那么接下来我们就捂住下面，只看上半部分的，来证明 $\S{ABE}+\S{ABG}$ 为定值。

设 $\odot O$ 与 $AB$ 切于 $H$，大圆半径为 $R$，小圆半径 $OH=r$，则有 $(R-r)^2=r^2+QH^2$，那么
\begin{align*}
\S{ABE}+\S{ABG}&=R(BE+AG)\\
&=2R^2(\tan\angle BAE+\tan\angle ABG)\\
&=2R^2\left(\frac r{HA}+\frac r{HB}\right)\\
&=4R^3\cdot\frac r{HA\cdot HB}\\
&=4R^3\cdot\frac r{(R+QH)(R-QH)}\\
&=4R^3\cdot\frac r{R^2-(R-r)^2+r^2}\\
&=2R^2.
\end{align*}

乌贼

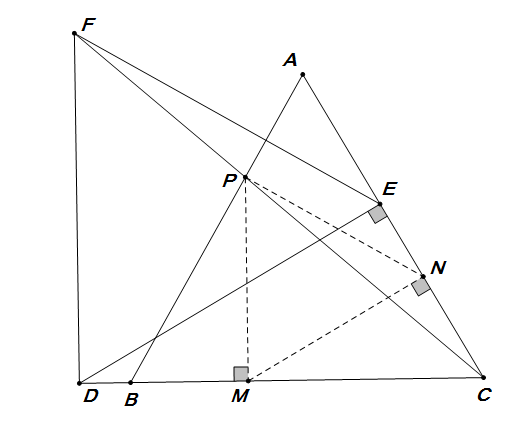
易证$ \triangle DEF $为正三角形，有\[ DF=DE \]作$ PM\perp BC $于$ M $，$ MN\perp AC $于$ N $，得\[ \angle PMN=60\du  \]又$ DM\px DF,MN\px DE $有\[ \dfrac{PM}{FD}=\dfrac{CM}{CD} =\dfrac{MN}{DE}\riff PM=MN\]即$ \triangle PMN $为正三角形，故\[ \angle APN=90\du  \]所以\[ \triangle APN\cong \triangle BMP\riff \dfrac{AP}{PB}=\dfrac{MB}{PB} =\dfrac{1}{2}\]