|
|
Last edited by 走走看看 2017-12-3 16:14

这道题,按以下方式建立空间直角坐标系,计算B、D‘的坐标,却发现结果不行。
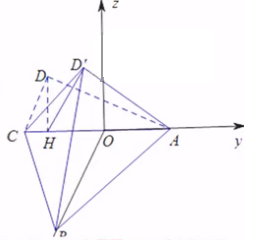
$设D'(x,y,z),则OD’=\frac{1}{2}AC=\frac{\sqrt{6}}{2},AD'=AD=\sqrt{5},A(0,\frac{\sqrt{6}}{2},0),B(\frac{\sqrt{30}}{2},0,0)。$
即:
$x^2+y^2+z^2=\frac{6}{4}$
$x^2+(y-\frac{\sqrt{6}}{2})^2+z^2=5$
$解得 y=-\frac{2}{\sqrt{6}},则D'可表示为(x,-\frac{2}{\sqrt{6}},\sqrt{\frac{5}{6}-x^2})。$
$\vv {BD'}=(x-\frac{\sqrt{30}}{2},-\frac{2}{\sqrt{6}},\sqrt{\frac{5}{6}-x^2})。$
$\vv {CA}=(0,1,0)。$
$|cosθ|=\frac{\frac{2}{\sqrt{6}}}{\sqrt{-\sqrt{30}x+9}}。$
$得不到\frac{\sqrt{6}}{6}。$ |
|