|
|
 战巡
战巡
posted 2017-12-8 01:55
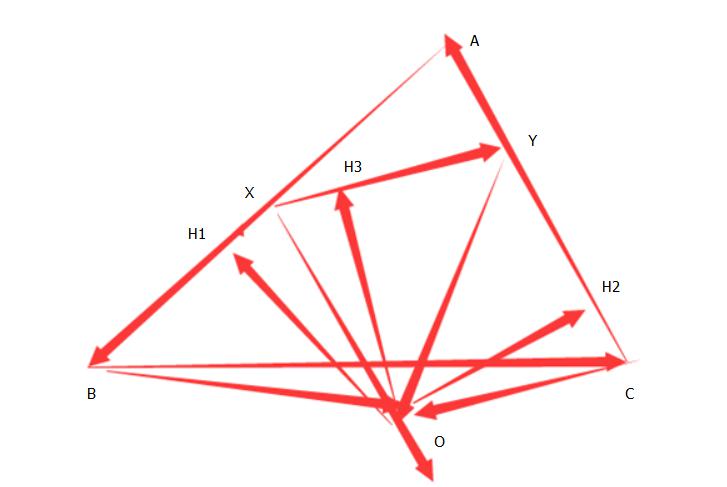
随手画的图,凑合看吧,作图过程没画完全,但不难理解
如图,$△ABC$确定,作$BC$中垂线$MO_1$,且在上面与$A$点同侧方向上找出一点$O_1$,使得$∠BO_1C=\pi-3(\pi-∠A)$
以$O_1$为圆心,$O_1B$为半径作圆$O_1$
作$∠A$平分线$AO$,与圆$O_1$交于$O$,连$OB, OC$
作$∠COX=∠BOY=\pi-∠A$
则$X, Y$即为所求点
证明:
过$O$作$BX, CY, XY$垂线,分别交于$H_1, H_2, H_3$
显然$OH_1=OH_2$,且易证$∠BOX=∠XOY=∠YOC=\frac{\pi-∠A}{2}$,$∠H_1OH_2=\pi-∠A=∠COX=∠BOY$,有$∠XOH_1=∠COH_2$,继而可证$△XOH_1\simeq△COH_2$,$CO=XO$
同理可证$YO=BO$
如此可知$△BOX\simeq △XOY\simeq △COY$,$BX=XY=CY$ |
|