求证：三角形内切圆中的角相等

lvhuiwang

已知，△ABC的内切圆与三边BC、AC、AB相切于D、E、F，M是EF的中点，
求证：∠EDM=∠ADE。

kuing

结论写错了吧？应该是 ∠EDM=∠ADF

kuing

证明：过 $A$ 分别作 $DE$ 和 $DF$ 的平行线交直线 $BC$ 于点 $P$ 和 $Q$，如图所示。



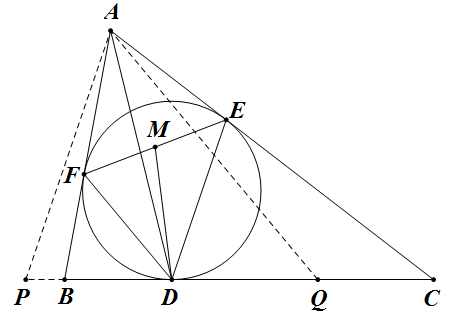
因为 $DP=EA=FA=DQ$，即 $AD$ 是 $\triangle APQ$ 的中线。

又因为 $\angle APQ=\angle EDC=\angle DFE$，同理 $\angle AQP=\angle DEF$，因此 $\triangle APQ$ 及其中线 $AD$ 与 $\triangle DFE$ 及其中线 $DM$ 整体相似，所以有 $\angle EDM=\angle QAD$，而由 $AQ\px DF$ 得 $\angle QAD=\angle ADF$，即结论得证。

本帖最后由 kuing 于 2018-2-18 17:58 编辑

lvhuiwang

很好的方法。就是现教材没有弦切角等于它所夹的弧所对的圆周角定理，要多几步证明。图中有了两个M点。原题中的图不好上传，原图的M点在AD的左侧。

kuing

回复 4# lvhuiwang

对喔，忘了那中点也是M，还好程序还没关，回头改改。

至于中点M在AD的左还是右都是一样的。

kuing

改好了。

其妙

回复 3# kuing
现在都不会平面几何题了

Tesla35

这个就是陪位中线啊。

kuing

回复 8# Tesla35

过程写写看呀？

乌贼

引理：直角$ \triangle ABC $中，$ \angle ACB=90\du  $，$ C $在$ AB $上的垂足为$ D $，$ P $为以$ B $为圆心，$ BC $为半径的园$ B $上任一点，$ AB $交园$ B $于E，则$ PE $平分$ \angle APD $。
上述问题为其特殊点，但引理不好证明

isee

回复 10# 乌贼


    设直线AB与圆B的另一个交点是F，则，A，D，E，F 四点为调和点列，PE与PF自然就分别是$\angle DPA$的内外角分线了。

乌贼

回复 11# isee
对调和点不熟悉

isee

回复 12# 乌贼


    楼主的题一看是竞赛题，属正常的。这玩意平时用得极少。

    另外，春节好！

kuing

回复 10# 乌贼

你的意思是原题中的点D可以改成内切圆上任意一点？

PS、一会圆一会园

乌贼

回复 14# kuing
对

kuing

回复 15# 乌贼

不过其实也一样，3#的图中，A、E、F、M 及内切圆固定，D 运动，而 BC 保持与圆切于 D，如下图，结果还是那样（包括我的辅助线），因此可以说原题目也不算是特殊点。



又或者说，这就是你10#引理的一种证法，辅助线还是那样作：



当然了，这并不是个好的证法，画出来太多线不好看，我只是在说明它们本质相通，并不是特殊点。

乌贼

回复 16# kuing
你想多了

lvhuiwang

这的软件我不会用，数学符号输入不了。我只会用数学公式编辑器，画图用几何画板。我原思路是找圆心，再延长DM交圆，然后通过弧、圆心角、圆周角的等量关系来证，走不通。

lvhuiwang

回复 16# kuing


利用平行线构造等腰又相似的三角形把已知条件串起来了。巧妙的很！

乌贼

回复 10# 乌贼
证引理：如图

   设$ AP $与园$ B $另一交点为$ Q $，有\[ \triangle ABC\sim \triangle CBD\riff\dfrac{CB}{BD}=\dfrac{AB}{CB}=\dfrac{AB}{QB}=\dfrac{QB}{DB}\riff\\\triangle QBD\sim \triangle ABQ\riff\angle BQD=\angle BAQ=\angle 1\riff\\\angle QDA=\angle 3=\angle 1+\angle 2= \angle PQB=\angle BPQ\]即$ PQDB $四点共圆得\[ \angle QPD=\angle QBD \]又\[ \angle QPE=\dfrac{1}{2}\angle QBE=\dfrac{1}{2}\angle QBD=\dfrac{1}{2}\angle QPD \]所以$ PE $平分$ \angle APD $