等腰三角形中的角关系与线段关系

isee

如图，在$\triangle ABC$中，$AB=AC$，$D$底边$BC$上一点，$E$是线段$AD$上一点，且$\angle BED=2\angle CED=\angle BAC$.
求证：$BD=2 CD$.

abababa

设$AD$交$\triangle ABC$外接圆于$T$，作$EP$平分$\angle BET$交$BT$于$P$
由于$\angle BET=\angle BAC, \angle BTE=\angle BCA$，所以$\angle TBE=\angle CBA$
所以$\angle TBE=\angle BTE$，而$EP$平分$\angle BET$，所以$BP=TP$
由于$AB=AC$，所以$\angle PTE=\angle CTE$，而$\angle CET=\frac{\angle BET}{2}=\angle PET$，所以$\triangle CET \cong \triangle PET$
所以$TP=TC$，所以$BT=2TC$
而$\angle BTD=\angle CTD$，所以$\frac{BD}{CD}=\frac{BT}{CT}=2$，即$BD=2CD$

isee

回复 2# abababa


    继续继续，据说此题的证明有二十多种，平几中的几乎所有方法都可用上

乌贼

三个共圆搞定

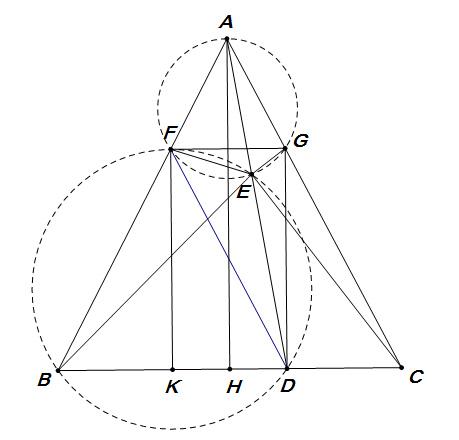
$ BDE $外接圆交$ AB $于$ F $，$ AFE $外接圆交$ AC $于$ G $，有\[ BFD=\angle BED=\angle BAC\riff FD\px AC\riff FB=FD \]\[ \angle AGF=\angle AEF=\angle ABC=\angle ABC\riff FG\px BC \]又\[ \angle AEG=\angle AFG=\angle ACB \]所以$ EGCD $四点共圆，$ H $为$ BC $中点，$ K $为$ BD $中点，有\[ \angle CGD=\angle CED=\angle CAH\riff FK\px AH\px DG \]故$ FGCD,FGDK $都为平行四边形，有\[ CD=FG=KD=\dfrac{1}{2}AD \]

isee

回复 2# abababa


回复 4# 乌贼

鼓掌！