来自减压群的圆外一点作两垂线求四边形最大面积

kuing

生如夏花(2365*****) 10:56:18
过圆 $\Gamma: x^2+y^2=4$ 外一点 $P(2,1)$ 作两条互相垂直的直线 $A B$ 和 $C D$ 分别交圆 $\Gamma$ 于 $A, ~ B$和 $C, ~ D$ 点，则四边形 $A B C D$ 面积的最大值为
@大色k 15题，应该可以直接用扫过面积的运动法，快速判断出AB=CD时，取到最大值么？

运动法我觉得这个四边形变化的东东太多，不太好说明增减，猜答案尚可，证明还是算了。

还是来写个常规方法吧，反正也是简单的。

首先说明一下，这题其实应该交待清楚ABCD的位置，或者配个图，
否则，字母这样标

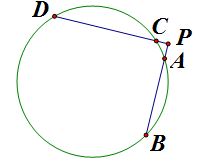
也是说得过去的，因为你也没说ABCD必须是凸四边形，交叉的四边形也算是四边形，而且也有面积。

现在就按命题者的原意来画，并过圆心作两直线的垂线，如下图。



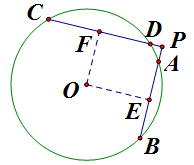
则有
\begin{align*}
S&=\frac 12PB\cdot PC-\frac 12PA\cdot PD\\
&=\frac 12(PE+EB)(PF+FC)-\frac 12(PE-EB)(PF-FC)\\
&=PE\cdot FC+PF\cdot EB\\
&\leqslant \sqrt {(PE^2+PF^2)(FC^2+EB^2)}\\
&=\sqrt {(PE^2+PF^2)(r^2-OF^2+r^2-OE^2)}\\
&=OP\sqrt {2r^2-OP^2},
\end{align*}
当 $AB=CD$ 时取等。

其妙

将P点改在圆内的，例如P（1,1），其余不变，求ABCD面积最大值

色k

回复 2# 其妙

那就是FAQ了

其妙

将P点改在圆内的，例如P（1,1），其余不变，求ABCD面积最大值
其妙 发表于 2018-3-3 10:23

继续改，将P点改在椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$内的，其余不变，求ABCD面积最大值

isee

回复 4# 其妙

这就很“闲”——（有仿射为依据，圆透就椭圆通）——了，除非你的结论非常优美。

kuing

回复 5# isee

不通不通，仿射改变垂直。

isee

回复 6# kuing

但面积（比）是不变量，高等几何里多半有公式可套。。。。。至少何时最大，再说，哈哈。。。。

其妙

某网友的，将就看