函数

依然饭特稀

realnumber

第2小题，f(x1)+f(x2)=-5即$3=(e^{x_1}-x_1)+(e^{x_2}-x_2)$
当-1<x1<0时，$1<e^{x_1}-x_1<1+\frac{1}{e}$,得到$2-\frac{1}{e}<e^{x_2}-x_2<2$
从图中大致可得到$1<x_2<1.2$(注意，不是取值范围，只是个粗糙的估计)，这样x1-2x2>-4+1/e就成立了。

接下来，试着把这个思路过程写得更严密点，引入切线，割线来处理函数不等式。

realnumber

假设$x_2\ge 1.2$
则$e^{x_2}-x_2=ee^{x_2-1}-x_2>e(1+x_2-1)-x_2>1.7\times 1.2>2$与$e^{x_2}-x_2<2$矛盾
这样$x_2<1.2$
如此$x_1-2x_2>-1-2.4>-4+1/e$

依然饭特稀

我搞的前两行是一样的，x2的范围弄的复杂了，想直接奔着结果去。。。。

依然饭特稀

我搞的前两行是一样的，x2的范围弄的复杂了，想直接奔着结果去。。。。

realnumber

特别对“单峰”函数，函数就夹在切线和割线之间，可以缩小定义域提高精度
例如：$f(x)=e^x-\frac{5}{6}x^2-2x$,当$-1\le x \le 1$时,求证:$e-\frac{17}{6}\le f(x) \le \frac{5}{3}$
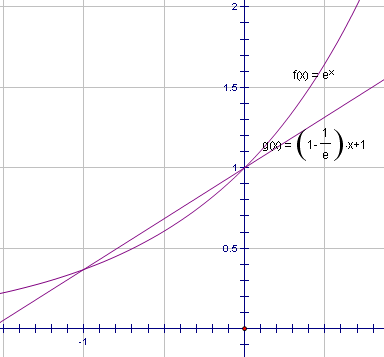
当$-1\le  x \le 0$时，$e^x\le  (1-\frac{1}{e})x+1$,只需要证$(1-\frac{1}{e})x+1\le \frac{5}{6}x^2+2x+\frac{5}{3}$,又$-\frac{1}{e}x\le -\frac{2}{5}x$
只需证$0\le \frac{5}{6}x^2+\frac{7}{5}x+\frac{2}{3},-1\le x\le 0$,计算下判别式就 可以说明成立

lemondian

回复 2# realnumber
这真是一个蛮好的思路，就是考试时，没法画图，如何得到x2<1.2是困难的哩。

lemondian

realnumber

也许要大胆猜，由要证明的去猜，毕竟比较宽松