证明线段相等

player1703

在Rt$\triangle$ABC中, $\angle$C=90$\du$. CH是斜边上的高. 分别作AH, HB的中垂线交DB于D, E. 延长DB至F使得DE=EF. BD$\perp$BG且FH = FG.
求证BC=BG.

isee

回复 1# player1703

这个图也是，条件也是分散，上解析强算吧。





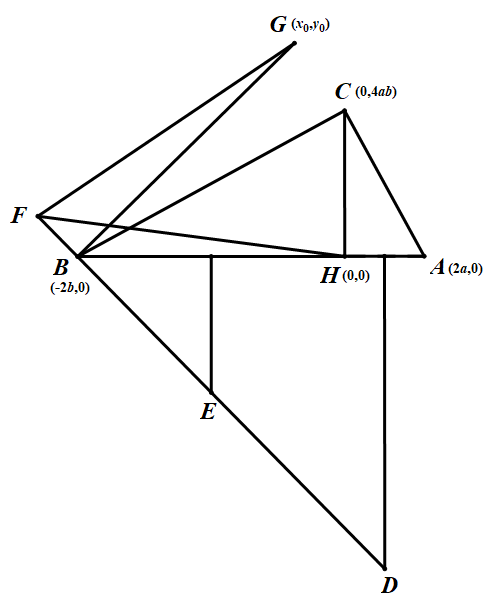
如图，以$H$点为坐标原点，$HA$，$HC$所在的直线分别为$x$轴，$y$轴建立直角坐标系。

不妨设$B(-2b,0)$，$A(2a,0)$，由直角三角形斜边上的高，可知$C(0,2\sqrt{ab})$（图中写错了，注意，不改了），方便书写记$c=2\sqrt{ab}$。

设$BD$直线方程为$$x+2b+\lambda y=0,$$
则$BG$直线方程为$$\lambda(x+2b)-y=0,$$
点$D,E$均在直线$BD$上容易求得$$D(a,-(a+2b)/\lambda),E(-b,-b/\lambda),$$
由$E$是$DF$的中点，得$$F(-a-2b,a/\lambda).$$

设点$$G(x_0,y_0)，$$则有$$\lambda(x_0+2b)-y_0=0$$成立。

由$\abs{FH}=\abs{FG}$得到$$(a+2b)^2+(a/\lambda)^2=(x_0+a+2b)^2+(y_0-a/\lambda)^2,\Rightarrow x_0^2+4bx_0+y_0^2=2ay_0/\lambda-2ax_0,$$
欲证$$\abs{BG}=\abs{BC}\iff (x_0+2b)^2+y_0^2=4b^2+c^2=4b^2+4ab\iff x_0^2+4bx_0+y_0^2=4ab.$$
即需证$$2ay_0/\lambda-2ax_0=4ab\iff \lambda(x_0+2b)-y_0=0,$$
这是显然成立的。