一道幾何 證線段相等

231908

kuing

真难，搞了一个多小时才勉强撸了出来，证法还不太好看，或许，是我变渣了……

首先，为了搞这道题我临时搞出了如下引理：

引理：如上图所示，则有
\[\frac{EA}{EB}=\frac{\cot\angle1+\cot\angle2}{\cot\angle3+\cot\angle4}.\]

时间关系，引理的证明等我有空再写。

回到原题，如下图：

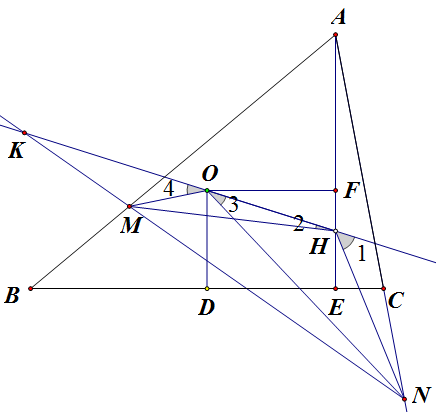
由 `O`, `H`, `C`, `N` 四点共圆得
\begin{align*}
\angle1&=\angle OCA=90\du-B,\\
\angle3&=\angle HCA=90\du-A,
\end{align*}
同理，由 `O`, `H`, `B`, `M` 四点共圆得
\begin{align*}
\angle2&=\angle OBA=90\du-C,\\
\angle4&=\angle HBA=90\du-A,
\end{align*}
于是，由引理得
\[\frac{KH}{KO}=\frac{\tan B+\tan C}{2\tan A}.\]

要证明 `KA=KH`，即证 `K` 的 `AH` 上的射影为 `AH` 的中点，由此可见，只需证明
\[\frac{KH}{KO}=\frac{AH/2}{AH/2-HF},\]
熟知 `AH=2OD`，由此可得 `AH/2-HF=AE-2OD`，因此
\[\frac{AH/2}{AH/2-HF}=\frac{OD}{AE-2OD}=\frac{R\cos A}{2R\sin B\sin C-2R\cos A}=\frac{\cos A}{2\cos B\cos C},\]
所以只需证明
\[\frac{\tan B+\tan C}{\tan A}=\frac{\cos A}{\cos B\cos C},\]
而这也是熟知的`\Box`

乌贼

引理；$ O,H $分别为$ \triangle ABC $的外心和垂心，$ AH $交$ BC $于$ E $，$ F $为$ OH $中点。求证：$ \angle OAD=\angle FDH $
证明：如图\[ \angle GBE=\angle CAE=\angle CBH \]所以\[ \triangle HBD\cong \triangle EBD \riff HD=DE \riff DF\px OE\\ \riff \angle FDH=\angle OEH=\angle OAH\]

下面证明原题：见图\[ \angle MBO=\angle BAO=\angle HAC=\angle HBC\riff OM=HF\riff OH\px MF \]又\[ ACH=\angle HMN=\angle OCB=\angle OCG\riff OG=HN\riff OH\px GN \]知$ OH $的垂直平分线过$ CB $与$ MN $的交点$ P $且交$ AH $于$ R,T $为$ OH $中点
由$ TPDH $四点共圆有\[ \angle RHT=\angle TPD=\angle TPK \]故$ RKPH $四点共圆得\[ \angle RKH=\angle RPH=\angle TDH \]由引理知\[ \angle RKO=\angle TDH=\angle OAR \]因此$ AKTR $四点共圆所以有\[ \angle KAR=\angle ROH=\angle RHO \]$ 则\triangle AKH $为等腰三角形\[ AK=HK \]