三角形内外心连线与AD平行

郝酒

三角形ABC，内心为I，外心为O，弧ACB的中点为E，弧ABC的中点为F，在圆内选一点D，使三角形DEF与三角形ABC相似，求证：AD//OI.


D点位置要怎么刻画呢？

Tesla35

这都是谁发现的

郝酒

四边形相似用得妙啊：）
对了，四个角对应相等的四边形是相似的吧？感觉不太会证呢：）

kuing

回复 2# Tesla35

谁发现的，不知道……
上面的证明是谁的，也不知道……

isee

这个倒是倒是好玩

kuing

像上面这么巧妙的辅助线我是想不出来嘀，我只会使用...暴...力……靠着各种工具总算强行证了出来……

下面的证法中，包含了几何、坐标、向量、三角，真 TM 渣渣……

首先建立平面直角坐标系，使得外心 `O` 为原点且 `BC` 平行于 `x` 轴，不失一般性，设外接圆的半径 `R=1`，则不难得出 `A`, `I` 的坐标分别为
\begin{gather*}
A\bigl(\sin(C-B),\cos(B-C)\bigr),\\
I(\sin C-\sin B,r-\cos A),
\end{gather*}
难点是求 `D` 的坐标，正如楼主说“D点位置要怎么刻画呢？”，单靠计算不容易，所以要用点几何法。



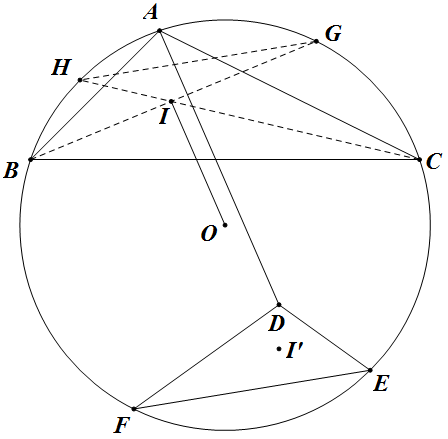
如图，其中 `I'` 为 `\triangle DEF` 的内心，则易知 `\triangle I'EF` 与 `\triangle IHG` 关于 `O` 中心对称。

易知 `AI\perp HG`，所以 `AI\perp EF`，故由 `\triangle DEF\sim\triangle ABC` 可知 `DI'\perp BC`，故此，要刻画 `D` 就只需计算 `DI'` 的长度即可，而
\[\frac{DI'}{AI}=\frac{EF}{BC}=\frac{GH}{BC}=\frac{\sin\frac{B+C}2}{\sin A}=\frac1{2\sin\frac A2},\]
所以
\[DI'=\frac{AI}{2\sin\frac A2}=\frac r{2\sin^2\frac A2},\]
这样就可以写出 `D` 的坐标了，但这里不写，用一下向量就不需要写了。

要证明 $AD\px OI$，即证 $\vv{DA}\times\vv{OI}=\bm0$，而 $\vv{DA}=\vv{OA}-\vv{OI'}-\vv{I'D}$，所以等价于证 $\bigl(\vv{OA}-\vv{I'D}\bigr)\times\vv{OI}=\bm0$，即证
\begin{gather*}
\left( \sin(C-B),\cos(B-C)-\frac r{2\sin^2\frac A2} \right)\times(\sin C-\sin B,r-\cos A)=\bm0,\\
\sin(C-B)(r-\cos A)=(\sin C-\sin B)\left( \cos(B-C)-\frac r{2\sin^2\frac A2} \right),\\
\cos\frac{B-C}2(r-\cos A)=\sin\frac A2\left( \cos(B-C)-\frac r{2\sin^2\frac A2} \right),
\end{gather*}
记 `p=\sin\frac A2`, `q=\cos\frac{B-C}2`，上式即
\[q(r-1+2p^2)=p\left( 2q^2-1-\frac r{2p^2} \right),\]
化简后即证
\[r=2p(q-p)=2\sin\frac A2\left(\cos\frac{B-C}2-\sin\frac A2\right),\]
展开后正是熟知的恒等式
\[\frac rR=4\sin\frac A2\sin\frac B2\sin\frac C2,\]
即得证。

kuing

PS1、为了撸这个证明，消耗了我很多脑细胞，昨晚就开始想了，后来看到上面的几何证法，简直太难想，就想放弃了，今天起来不甘心继续想，再.暴.力也要把它撸出来，结果就成上面那样子了……
PS2、最近连撸了三道几何题，都用到了同一个恒等式 `\frac rR=4\sin\frac A2\sin\frac B2\sin\frac C2`，真神奇……

isee

回复 7# kuing

我只能另解（非平几）一下你看不上眼的。。。。。。

郝酒

真暴力，有一步不是太清楚："则易知△I′EF与△IHG关于O中心对称。"
可以看出E和H，F和G是关于O对称的，I和I’为什么关于O对称呢？

kuing

回复 9# 郝酒

`\angle I'EF=\frac12\angle E=\frac12\angle B=\angle IHG`，另一对角同理，所以……

郝酒

回复 10# kuing

谢谢ku版.

kuing

唔，其实不用向量也可以。

在得出 `I`, `I'` 对称、`DI'\perp BC` 以及 `DI'=\frac r{2\sin^2\frac A2}` 之后，再作两条辅助线如下图：



那么要证平行就只需证 `AL=DI'`，由于直线 `OI` 的方程为
\[y=\frac{r-\cos A}{\sin C-\sin B}x,\]
故根据 `A\bigl(\sin(C-B),\cos(B-C)\bigr)` 即得
\[AL=\cos(B-C)-\frac{r-\cos A}{\sin C-\sin B}\sin(C-B)=2q^2-1-(r-1+2p^2)\frac qp,\]
其中 `p`, `q` 如 6# 所设，于是只需证明
\[\frac r{2p^2}=2q^2-1-(r-1+2p^2)\frac qp,\]
后同 6#。

这样写起来就比 6# 好一些，不过要多画点线，也不怎么划算。

kuing

唔唔，再改用几何方法来求楼上的 `AL`，这样就连坐标系也可以扔掉了，当然了，这又要多画两线了。



如图，则有
\[\frac{AL}{AI}=\frac{MO}{MI}=\frac R{AM-AI}=\frac R{2R\cos\frac{B-C}2-\frac r{\sin\frac A2}},\]
而在 6# 已经有
\[\frac{DI'}{AI}=\frac1{2\sin\frac A2},\]
所以要证 `AL=DI'` 只需证
\[2R\cos\frac{B-C}2-\frac r{\sin\frac A2}=2R\sin\frac A2,\]
整理后依然还是
\[r=2R\left( \cos\frac{B-C}2-\sin\frac A2 \right)\sin\frac A2,\]
所以就OK了。

这回的改进还算划算，整个过程下来简洁了不少，连 `p`, `q` 也没了，已经比较几何化了，就差三角还没扔。

abababa

3楼的这个证明我还是不懂。四个角对应相等，四边形不一定相似，例如正方形和一般矩形就不相似，必须四条边对应成比例才行。
还有最后一步，得到比例相等，怎么就平行了呢？还应该证明$JD \sslash OG$才行，这样才能说另一组边也平行。
感觉这两个都不好证。

kuing

回复 14# abababa

俩四边形相似是因为 `\triangle ABC\sim\triangle DEF` 以及 `\triangle JBC\sim\triangle JEF`，合起来便得 `ABJC\sim DEJF`，而并不是由四角对应相等得出的。

至于 $JD\px OG$ 这一点，也不难证啊，`\angle OGA=(B-C)/2=\angle IJC-\angle IJB=\angle DJA`。

我自己是这样看的，也说不定有更简单直接的理解方式。

abababa

回复 15# kuing

谢谢，四边形相似的那个明白了，下面那个导角的$(B−C)/2=\angle IJC-\angle IJB$我导了半天才导出来，最后化为弧$BC=BC$才弄出来的，可能是我有一些基本结论不知道。

kuing

回复 16# abababa

`BICJ` 共圆 `B/2=\angle IBC=\angle IJC`

abababa

回复 17# kuing
谢谢，原来是用到旁心对边的张角公式，我对旁心不熟悉，很多东西都不知道。