直角三角形内心I，已知角GIF为45度，证垂直

郝酒

如题，感觉很巧妙：）

战巡

如图，作$DH⊥BC$，$∠BIG=∠BIN, ∠CIF=∠CIM$

易证$△ACD≌△CDH$，有$\tan∠DFH=\frac{DH}{HF}=\frac{DH}{CH-CF}=\frac{AD}{AC-CF}$
同理有$\tan∠EGC=\frac{AE}{AB-BG}$
于是如果要证明$DF⊥GE$，只要证$∠DFH+∠EGC=90°$，也就是$\tan∠DFH·\tan∠EGC=1$

又易证$△BGI≌△BDI，△CIF≌△CIM$，有$AC-CF=AC-CM=AM，AB-BG=AB-BN=AN$，要证明的东西就变成$\tan∠DFH·\tan∠EGC=\frac{AD}{AN}·\frac{AE}{AM}=1$
另一方面，易证$∠NIM=135°$，加上$IN=IG，IM=IF$，有$S_{△GIF}=\frac{1}{2}\sin(45°)IG·IF=\frac{1}{2}\sin(135°)IN·IM=S_{△NIM}$
那么易证$S_{△ANM}=S_{△ABC}-S_{△NIM}-S_{△NIB}-S_{△MIC}-S_{△BIC}=S_{△ABC}-2S_{△BIC}$
不难证明同样有$S_{△ADE}=S_{△ABC}-2S_{△BIC}$，因此$S_{△ADE}=S_{△ANM}$，然后$\frac{AD}{AN}·\frac{AE}{AM}=1$

郝酒

回复 2# 战巡
谢谢战版，有一步感觉不是很显然，三角形ADE的面积等于三角形ABC的面积减去2倍的三角形BIC的面积。

这个只对直角三角形成立，做法还是截全等，导面积。

乌贼

设$ T $为$ DF $与$ EG $的交点，分别作点$ D,E $在$ BC $上的垂足$ M,N $,作$ IP\perp IF $交$ DM $于$ P $，作$ IQ\perp IG $交$ EN $于$ Q $，连接$ PF,QG,PG,QF $。$ K $为$ PF $与$ QG $的交点。则$ \triangle IMN $为等腰直角三角形。又$ IPMF $四点共圆，有$ \triangle IPF $为等腰直角三角形，同理$ \triangle IQG $为等腰直角三角形。
  易知$ IPGK $四点共圆（$ \angle IPK=\angle IGK=45\du  $），$ IQFK $四点共圆（$ \angle IQK=\angle IFK=45\du  $），又$ IGNQ $四点共圆，所以\[ \angle QIN=\angle QGN=\angle KQF=\angle KIF\\\riff \angle KIN=\angle FIQ=45\du  \]故\[ \angle IFM=\angle PFM+45\du =\angle GPK+45\du =\angle GIK+45\du =\angle GIN \]有\[ \triangle MIF\sim \triangle NIG\riff \dfrac{IM}{GN}=\dfrac{MF}{IN} \]又\[ \triangle IBM\sim \triangle CIN\riff \dfrac{IM}{BM}=\dfrac{CN}{IN} \]\[ \triangle DMB\sim \triangle CNE\riff \dfrac{DM}{BM}=\dfrac{CN}{EN} \]因此有\[ \dfrac{DM}{MF}=\dfrac{GN}{EN} \]即\[ \triangle DFM\sim \triangle GEN\\\riff\angle TFG=\angle GEN \]得$ TENF $四点共圆有\[ \angle ETF=\angle ENF=90\du  \]

isee

回复 4# 乌贼


哦，最近用四点共圆频繁极了。。。中没细看细看。。。

kuing

回复 4# 乌贼

这图形让我想起那道经典的等腰直角里45度证平方和的那道题，用的旋转证的那个。

kuing

三角法又来了

首先如下图：

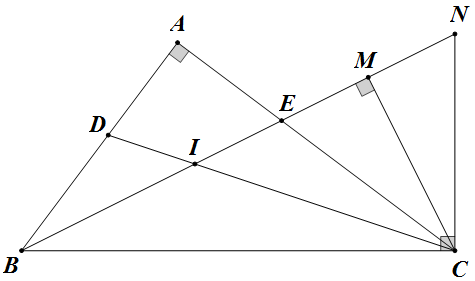
易知 `MI=MC` 且 `CE=CN`，记 `BC=a`，则
\[BI=a\cos\frac B2-a\sin\frac B2,CE=a\tan\frac B2.\]

回到原题上，记 `\angle BIG=x`, `\angle CIF=y`，则 $x+y=90\du$，又记 `\angle BFD=w`, `\angle CGE=z`，如下图：

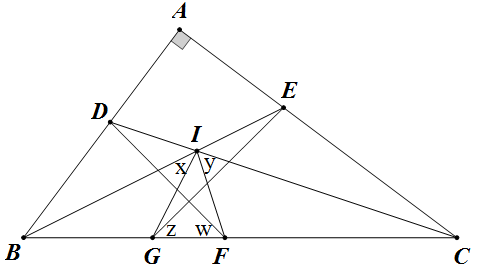
则由正弦定理得
\[BG=\frac{\sin x}{\sin\left( \frac B2+x \right)}BI=\frac{a\cos\frac B2-a\sin\frac B2}{\sin\frac B2\cot x+\cos\frac B2}=\frac{1-\tan\frac B2}{\tan\frac B2\cot x+1}\cdot a,\]
则
\[CG=a-BG=\frac{\tan\frac B2(\cot x+1)}{\tan\frac B2\cot x+1}\cdot a=\frac{\cot x+1}{\tan\frac B2\cot x+1}\cdot CE,\]
所以
\[\frac{\cot x+1}{\tan\frac B2\cot x+1}=\frac{CG}{CE}=\frac{\sin(z+C)}{\sin z}=\cos C+\cot z\sin C,\]
解得
\[\cot z=\frac{\cot x+1-\cos C\left( \tan\frac B2\cot x+1 \right)}{\sin C\left( \tan\frac B2\cot x+1 \right)},\]
由半角公式有
\[\tan\frac B2=\frac{1-\cos B}{\sin B}=\frac{1-\sin C}{\cos C},\]
代入上面的分子中，即得
\[\cot z=\frac{\sin C\cot x+1-\cos C}{\sin C\left( \tan\frac B2\cot x+1 \right)}=\frac{\cot x+\tan\frac C2}{\tan\frac B2\cot x+1},\]
同理有
\[\cot w=\frac{\cot y+\tan\frac B2}{\tan\frac C2\cot y+1},\]
由于 `\cot y\cot x=1`，从而
\[\cot w=\frac{1+\cot x\tan\frac B2}{\tan\frac C2+\cot x}=\frac1{\cot z},\]
可见 $w+z=90\du$，即得证。

isee

乌贼在4#真是精彩，总是能从无处生有，妙笔生花。
不过，乌贼每次的辅助线都是一团一团的，令人眼花缭乱。

把乌贼辅助从另一个角度说再写一次，主要是倒相似三角形的方式略不同。



题：$I$是$\triangle ABC$的内心，$\angle A=90^\circ$，$\angle GIF=45^\circ$.
求证：$DF\perp GE$.

证：分两步，第一步是准备。

注意到$CD$为$\text{Rt}\triangle ABC$的锐角角分线，过点$D$作$DM\perp BC$于$M$，则由对称性，知$$IM=IA,\angle IMC=45^\circ.$$
同理，点$E$在$B$C上的射影为$N$，则$$IN=IA,\angle INB=45^\circ.$$
于是等腰$$\text{Rt}\triangle IMN,\angle MIN=90^\circ.$$

在$\text{Rt}\triangle ABC$中，由两垂线知$$\triangle DMB \sim \triangle CNE\Rightarrow BM\cdot NC=NE\cdot DM.$$

另一方面，在$\triangle IBC$中两底角和为$45^\circ$，且$\angle IBM+\angle BIM=45^\circ$，进一步，知$$\triangle BIM\sim \triangle ICN\Rightarrow BM\cdot NC=IM\cdot IN=IM^2.$$




下面是第二部分(图中也是全部的辅助线)，也就是6#提到的.

在等腰直角三角形$MIN$的直角共顶点一个$45^\circ$与此直角三角形r的斜边分别相交于点$G,F$，于是有熟知的(无需添辅助线，倒角即可)$$\triangle MIF \sim \triangle NGI\Rightarrow MF\cdot GN=IM\cdot IN=IM^2.$$

进一步$$NE\cdot DM=MF\cdot GN\Rightarrow \text{Rt}\triangle DMF \sim \text{Rt}\triangle GNE.$$

后同4#.

乌贼

回复 8# isee

   还可简化 ，作点$ D,E $在$ BC $上的垂足$ M,N $，$ P $为$ CD $与$ DN $的交点，$ T $为$ DF $与$ DG $交点。由对称性知$ \triangle IMN $为等腰直角三角形。\[ \angle MDI=\angle IPE=\angle NIE\riff \triangle MDI\sim \triangle NIE\riff\dfrac{DM}{IM}=\dfrac{IN}{EN}\\\triangle MIF\sim \triangle NGI\riff\dfrac{IM}{MF}=\dfrac{NG}{IG}\]有\[ \dfrac{DM}{MF}=\dfrac{NG}{EN}\riff\triangle MFD\sim \triangle NEG \]故$ ETFN $四点共圆，因此\[ \angle ETF=\angle ENF=90\du  \]