|
|
长风大侠 2018-10-22 10:40
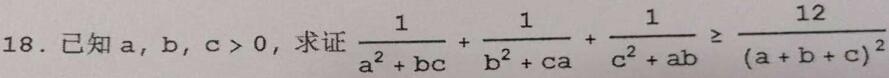
 ,只想出难看的: ,只想出难看的:
不妨设 `a=\min\{a,b,c\}`,先证明
\[\frac1{b^2+ca}+\frac1{c^2+ab}\geqslant\frac4{\frac34(b+c)^2+a(b+c)-bc}, \quad(*)\]
将上式去分母因式分解再配方后,等价于
\[(b-c)^2\bigl((b+c-2a)^2+2(b-c)^2+10bc-5ab-5ac\bigr)\geqslant0,\]
显然成立,于是,令 `b+c=t`,由式 (*) 及柯西,有
\[\sum\frac1{a^2+bc}\geqslant\frac1{a^2+bc}+\frac4{\frac34t^2+at-bc}\geqslant\frac9{a^2+\frac34t^2+at},\]
那么要证原不等式只需证
\[9(a+t)^2\geqslant12\left( a^2+\frac34t^2+at \right),\]
化简即 `3a(2t-a)\geqslant0`,由于 `t\geqslant2a`,所以不等式得证。
注:取等条件为 `a=0` 且 `b=c` 及其轮换,所以依照原题的正数条件是取不了等的。 |
|