二元函数最值

guanmo1

敬畏数学

回复 1# guanmo1
好像有点图形味道，但还是没有结果。

huing

回复 2# 敬畏数学
三角形的周长，三个顶点为$(a,a),(0,b),(1,3)$

huing

问题转化为：在y轴和大斜线x=y上各找一动点，与定点(1,3)形成一个三角形，求其周长的取值范围。
周长显然只有下界，没有上界。
按费马最小光程原理，最小三角形是一个光回路三角形。

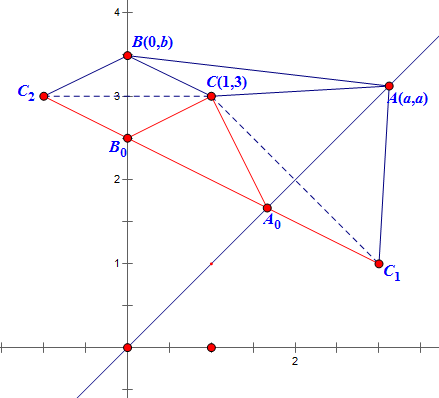
如图，作定点$C(1,3)$关于y轴和大斜线$x=y$的镜像点$C_1(3,1),C_2(-1,3)$,将周长$CA+AB+BC$转化为折线长$C_1A+AB+BC_2$,
显然$C_1A+AB+BC_2\geqslant C_1C_2$. 所以连结线段$C_1C_2$，取与y轴和大斜线的交点$A_0(5/3,5/3),B_0(0,5/2)$, 即得最小三角形$A_0B_0C$. 最小周长$C_1C_2=\sqrt{(3+1)^2+(1-3)^2}=2\sqrt{5}$.

敬畏数学

回复 4# huing
构造美妙！

其妙

问题转化为：在y轴和大斜线x=y上各找一动点，与定点(1,3)形成一个三角形，求其周长的取值范围。
周长显然只 ...
huing 发表于 2018-11-14 11:43

你是不是kuing的替身呀？
既然都知道是距离之和了，那就不必辛苦画图了，用向量模不等式或者闵科夫斯基不等式，亦或构造复数模，即可分分钟灭掉它！
$f(a,b)=\sqrt{(3-a)^2+(1-a)^2}+\sqrt{1^2+(b-3)^2}+\sqrt{a^2+(a-b)^2}
\hspace{3em} \geqslant\sqrt{[(3-a)+1+a]^2+[(1-a)+(b-3)+(a-b)]^2}$

说明：\hspace{3em}3个空格，
两个quad空格    \qquad
1个空格  quad空格
参考：blog.sina.com.cn/s/blog_4ddef8f80100iwwv.html

kuing

回复 6# 其妙

用空格干啥，用 align 系列环境写啊

其妙

回复 7# kuing
你这么快就回复了呀，我还想修改呢！这下不好 修改了，有痕迹了

huing

回复 6# 其妙
2#给了调子，要用图形嘛。有几何解释，可能更好吧。

俺不是kuing的化身，是kuing的粉丝。粉丝与偶像的解题风格有点不同呢。