香港奥数题 (2018)

kuing

回复 20# 业余的业余

是 2146。
对称性方面有空再考虑，现在我要搞一个特殊情形的结论来先——被除数为素数的情形。
鉴于如果结论是正确的话，或许以后会引用到，所以我决定等会开新帖来写。

业余的业余

回复 21# kuing

好的，期待。

kuing

回复 22# 业余的业余

forum.php?mod=viewthread&tid=5800，希望结论没问题，睡鸟……

tommywong

根據Kummer's theorem觀察和為2188的進位情況

100010001100       
2^4=16

這樣求出有16個k使$C_{2188}^k$不整除2

現在要求出k使$C_{2188}^k$整除2但不整除4

考慮只發生一次進位的情況，這種進位應該會剛好在1後面的0發生

000000000010
100010001010
2^3=8

000001000000
100001001100
2^3=8

010000000000
010010001100
2^3=8

這樣求出有24個k使$C_{2188}^k$整除2但不整除4

我想18#對p=2分析出來的應該就是這些結果

乌贼

回复 1# 业余的业余
想看看第三题2问答案

乌贼

第三题（1）
   如图：连接$ IE,IF,DK $，有\[ \angle IFE=\angle IEF=\angle IDK \]即$ FKID $四点共圆，又$ FIDC $四点共圆，所以$ FKIDC $五点共圆。得\[ \angle BKC=90\du  \]

乌贼

（2）先上一引理
       引理：$ P $为园$ O $外一点，直线$ PD $交园$ O $于$ C,D $两点，直线$ PB $交园$ O $于$ A,B $两点，$ AB $为园$ O $的直径，$ E $为$ AD $与$ BC $交点，$ E $在$ AB $上的垂足为$ F $，$ FE $延长线交$ CD $于$ G $，$ N $为$ AD $中点，$ M $为$ PN $与$ AC $交点。求证：$ MG\px AD $
      证明：

      如图：过$ C $点作$ CK\px MG $交$ PN $于$ K $，连接$ CF,DF,DB $，作$ DL\px CF $交$ AB $于$ L $。有$ \angle DLF=\angle GFA $
由\[ \triangle CMK\sim \triangle AMN\riff \dfrac{CM}{MA}=\dfrac{CK}{AN}=\dfrac{CK}{ND}=\dfrac{PC}{PD}=\dfrac{CF}{DL}\]因为\[ EC\perp CA\\EF\perp AB\\ED\perp DB \]有$ ACEF $四点共圆，$ EDBF $四点共圆，得\[ \angle CFA=\angle CEA=\angle DEB=\angle DFB\\\angle CFG=\angle DFG \]所以\[ \angle DLF=\angle CFA=\angle DFL\riff DF=DL \]即\[ \dfrac{CM}{MA}=\dfrac{CF}{DF} \]在$ \triangle FCD $中，由角平分线定理知\[ \dfrac{CF}{DF}=\dfrac{CG}{GD} \]综上有\[ \dfrac{CM}{MA}=\dfrac{CF}{DF}=\dfrac{CG}{GD}\riff MG\px AD \]
回到原题，
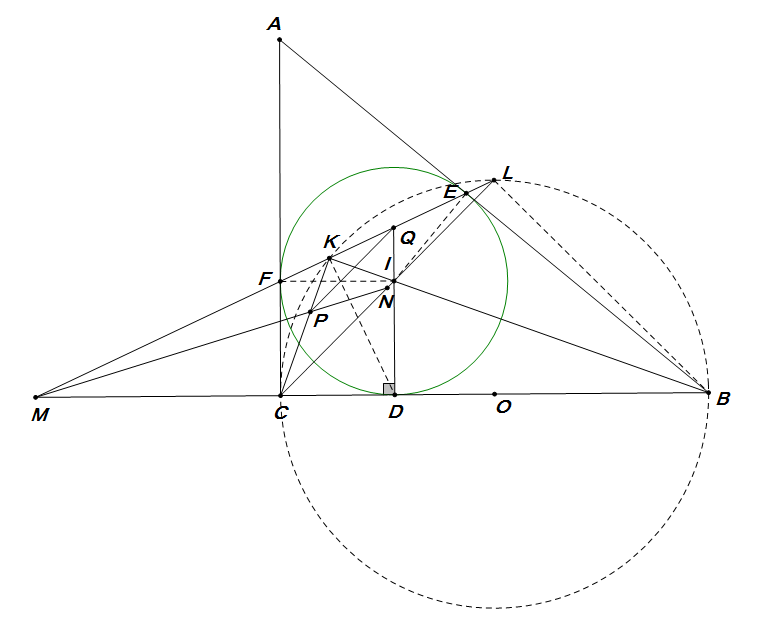
连接$ LB $，同理有\[ \angle CLB=90\du  \]
由引理知\[ PQ\px CL \]

业余的业余

强。谢谢各位！现沉不下心看数学，回头再来学习。