三角形四线交四边形面积

kuing

某大大问道：

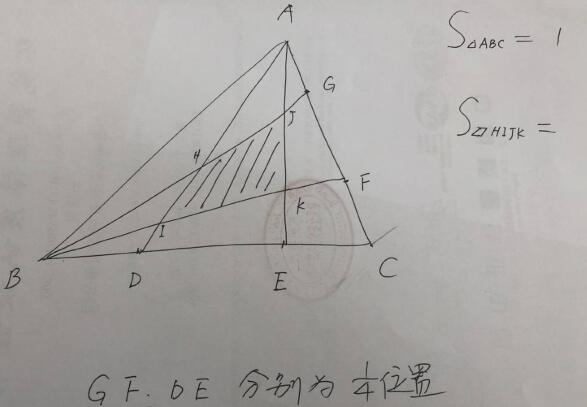
是不是有个梗

不知以前有没有写过，懒得找了，反正是简单东西，直接写个一般式，以后代数字好了。


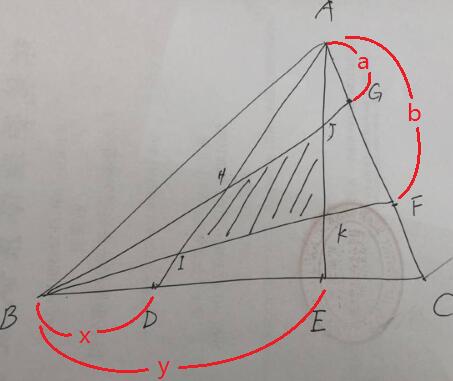
记 `AG:AC=a`, `AF:AC=b`, `BD:BC=x`, `BE:BC=y`，如图所示，则 $\S{ADE}=y-x$，由梅氏定理有
\[
\frac{AI}{ID}\cdot x\cdot\frac{1-b}b=1\riff\frac{AI}{AD}=\frac b{x(1-b)+b},
\]同理有
\begin{align*}
\frac{AK}{AE}&=\frac b{y(1-b)+b},\\
\frac{AH}{AD}&=\frac a{x(1-a)+a},\\
\frac{AJ}{AE}&=\frac a{y(1-a)+a},
\end{align*}而
\[
\frac{S_{HIKJ}}{\S{ADE}}=\frac{\S{AIK}-\S{AHJ}}{\S{ADE}}=\frac{AI}{AD}\cdot\frac{AK}{AE}-\frac{AH}{AD}\cdot\frac{AJ}{AE},
\]故
\[S_{HIKJ}=(y-x)\left( \frac{b^2}{\bigl(x(1-b)+b\bigr)\bigl(y(1-b)+b\bigr)}-\frac{a^2}{\bigl(x(1-a)+a\bigr)\bigl(y(1-a)+a\bigr)} \right),\]化简即得
\[S_{HIKJ}=\frac{(b-a)(y-x)\bigl(ab(x+y)+xy(a+b)-2abxy\bigr)}{(a+x-ax)(a+y-ay)(b+x-bx)(b+y-by)}.\]
对于原题，代 `a=x=1/4`, `b=y=3/4` 得 `128/455`。

realnumber

小奥六的内容，图中所画的（A为顶点的）三角形面积都可以算出来.

kuing

回复 2# realnumber

小奥方法怎么算？

realnumber

也是算出F分AE,CD的比例.他们好象用利用面积算的，不确定小奥有没有，添平行线三角形相似.

isee

回复 3# kuing

虽然没见到标答，但实质（面积比等价于线段比）不会发生变化

游客

是不是小学现在都可以“梅涅”了？