求一个向量表达式最小值

realnumber

$\vv{a}$,$\vv{b}$不相等,$\vv{c}$不为零向量，且$(\vv{c}-\vv{a})·(\vv{c}-\vv{b})=0$,
则$\frac{\abs{\vv{a}+\vv{b}}+\abs{\vv{a}-\vv{b}}}{\abs{\vv{c}}}$的最小值是_____.

kuing

由条件得
\[
\abs{\bm a+\bm b-2\bm c}=\abs{\bm a-\bm b},
\]故
\[
\frac{\abs{\bm a+\bm b}+\abs{\bm a-\bm b}}{\abs{\bm c}}
\geqslant \frac{2\abs{\bm c}-\abs{\bm a+\bm b-2\bm c}+\abs{\bm a-\bm b}}{\abs{\bm c}}=2,
\]取等显然不唯一，随便取一个可以是 `\bm a=(0,1)`, `\bm b=(0,-1)`, `\bm c=(1,0)`。其实，下图这样的都能取等：


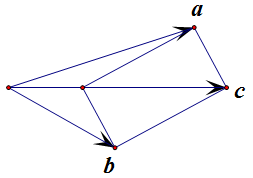
PS、单字母向量建议用粗体（\bm），这样好看些，特别是加绝对值 \abs 时。

敬畏数学

回复 1# realnumber
此题很简单的。OA=a,OB=b，OC=c，点C落在A、B为直径的圆上，|C|的最大值d+r=1/2（|a+b|+|a-b|）就为2.

kuing

回复 3# 敬畏数学

不是圆，是球（甚至是高维的），皆因题目没说是平面向量（凡向量题我都会注意看有没有平面二字没有的话我就尽量用像 2# 那样的纯向量解法比较稳妥）

isee

由条件得

这个$$\abs{\bm a+\bm b-2\bm c}=\abs{\bm a-\bm b},$$把题中那个垂直翻译得面目全非了，都又是和所求那么的接近……

kuing

回复 5# isee

这个其实就是矩形对角线相等呀……

业余的业余

回复 2# kuing

学习了。

$ \abs{\bm a+\bm b-2\bm c}=\abs{\bm a-\bm b}$

花了好久才想明白这个 :(

从几何意义上 位置向量 $\bm{a}$ 和 $\bm{b}$ 的中点 $\frac {\bm{a}+\bm{b}}2$ 到以 $\bm{a}$ 和$\bm{b}$ 为直径的圆上的一点代表的位置向量 $\bm{c}$ 的距离就是半径，就是 $\abs{\frac{\bm{a}-\bm{b}}2}$.

kuing

回复 7# 业余的业余

就是 $\bm x\cdot\bm y=0\iff\abs{\bm x+\bm y}=\abs{\bm x-\bm y}$ 代 `\bm x=\bm a-\bm c`, `\bm y=\bm b-\bm c`……