一个空间角比较的问题

力工

这个问题我是通过特殊位置角的大小来确定答案B的。

我想老实点解决它，问题中角$α$和$β$是容易比较的，但角$α$和$γ$如何通过计算比较出来，是个难题，想了几个晚上，都没定。
向各位高手求助。

业余的业余

第一感，角平分线定理，余弦定理。另 $AD:BD=k >1, B_1C $相同， 两个角用余弦定理表达出来，利用 余弦在区间内的单调性，可否得出结论。？

kuing

比较 `\alpha` 和 `\gamma` 其实与角平分线什么的都没关系，实际上就是：平面上一条直线被折起后的角 `\gamma` 不小于二面角 `\alpha`。

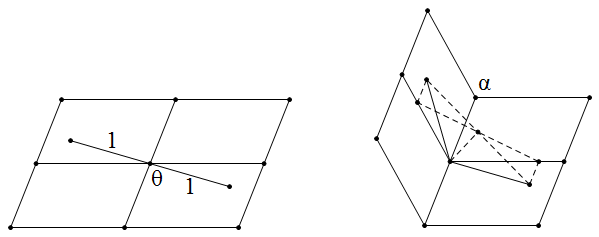
设直线与折痕所成夹角为 `\theta`，则有
\[\sin\frac\gamma2=\sqrt{\cos^2\theta+\left(\sin\theta\sin\frac\alpha2\right)^2},\]（推导细节我就懒得写了，请自行看图思考）那么显然有
\[\sin\frac\gamma2\geqslant\sqrt{(\cos^2\theta+\sin^2\theta)\sin^2\frac\alpha2}=\sin\frac\alpha2,\]所以 `\gamma\geqslant\alpha`，当且仅当 $\theta=90\du$ 时取等。

业余的业余

回复 3# kuing


   能否进一步推广到不一定是直线的情形: 比如图中的 $l$ 现在不是直线，在两个半边上分别有点 $A,B$, 如果$A,B$ 在折痕垂线的同一侧，那么折出来的角小于二面角，如果在折痕的异侧，那么折出来的角大于二面角？

kuing

能否进一步推广到不一定是直线的情形: 比如图中的 $l$ 现在不是直线，在两个半边上分别 ...
业余的业余 发表于 2019-3-16 21:19

未必，异侧时有也可能会小于，你想象一下极端情形：记中间那交点是 O，当 OA 几乎与折痕平行，OB 几乎与折痕垂直，这样无论怎么折，角 AOB 都接近直角，所以一开始折就会小于。

业余的业余

回复 5# kuing

是的。

kuing

回复 4# 业余的业余

进一步玩的话，可以了解一下三面角余弦定理。若利用该公式，则 3# 的情况还可以写成 `\cos\gamma=\sin^2\theta\cos\alpha-\cos^2\theta`，这显然更好看。

isee

回复 7# kuing

这个拿来求二面角，很多时候就把高考模拟题就秒了，经常用来对答案，我。

业余的业余

回复 7# kuing
好的，谢谢推荐。我有时间时一定去看。高考题都会有一些立体几何问题，有时候有巧招可省不少时间，更重要的是有智力愉悦感。

hjfmhh

回复 7# kuing 这是更加一般的结论

hjfmhh

回复 7# kuing

Kuing三面角余弦定理怎么说明，请书写一下。我是用向量说明的