求最短路径，猜了个光的折射

realnumber

在平面四边形ABCD中,$AB=BC=1,AD=CD=\sqrt{2}$,$\angle{DAB}=\angle{DCB}=Rt\angle{}$,点P为AD中点，
M,N分别在线段BD,BC上，则$PM+\frac{\sqrt{2}}{2}MN$的最小值为______.


利用折射猜了个答案，发现正好符合，此时ADB光速慢，比如水，CDB光速快，比如空气，当MN分别为中点时，符合折射定律$\frac{\sin a}{\sin b}=\frac{\sqrt{2}}{2}$，因此答案是$\frac{1}{2}+\frac{\sqrt{2}}{2}\frac{\sqrt{2}}{2}=1$,根据2楼提示修改下
函数导数办法不要，是初中题，有没平几办法？

kuing

过 `B` 作 `AD` 平行线 `l`，则 `\frac{\sqrt2}2MN\ge M` 到 `l` 的距离，最小值就是 `P` 到 `l` 的距离 `=1`？

isee

在平面四边形ABCD中,$AB=BC=1,AD=CD=\sqrt{2}$,$\angle{DAB}=\angle{DCB}=Rt\angle{}$,点P为AD中点，
M,N分 ...
realnumber 发表于 2019-3-20 14:28

光折射必然方向啊，只是要找到个几何意义罢了

realnumber

回复 2# kuing


    对答案应该是1，我忘了系数了

isee

过 `B` 作 `AD` 平行线 `l`，则 `\frac{\sqrt2}2MN\ge M` 到 `l` 的距离，最小值就是 `P` 到 `l` 的距离 `= ...
kuing 发表于 2019-3-20 14:43

火眼金睛

isee

招唤一下 乌贼

kuing

回复 6# isee

还招唤啥，不是已经解决了吗？
其实就是道很简单的平几题，而且题目给的数据和图形都比较特殊，算是很强的提示了……完全可以改成一般的

isee

回复 7# kuing

角度会不同。

主要是好久没看乌贼画图了~

isee

在平面四边形ABCD中,$AB=BC=1,AD=CD=\sqrt{2}$,$\angle{DAB}=\angle{DCB}=Rt\angle{}$,点P为AD中点，
M,N分 ...
realnumber 发表于 2019-3-20 14:28

"平面四边形"，高中卷中的？

kuing

续 7#：重点抽出来就是酱紫

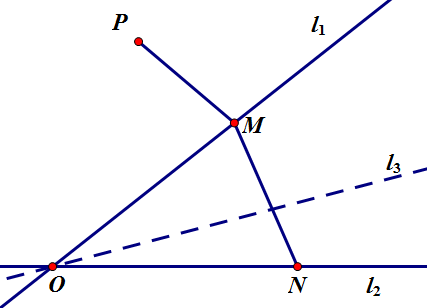
定点 `P`，动点 `M`, `N` 在定直线 `l_1`, `l_2` 上，求 `PM+kMN` 的最小值，过 `O` 作 `l_3` 使 `\sin\langle l_1,l_3\rangle=k\sin\langle l_2,l_3\rangle`，则 `PM+kMN\geqslant PM+kOM\sin\langle l_2,l_3\rangle=PM+OM\sin\langle l_1,l_3\rangle=PM+M` 到 `l_3` 的距离 `\geqslant P` 到 `l_3` 的距离。（要确保取等其实还需要限制一下 `P` 的位置，懒得扯了）

本帖最后由 kuing 于 2019-3-21 00:29 编辑

更正一下：过 `O` 作 `l_3` 使 `\sin\langle l_1,l_3\rangle=k\sin\langle l_1,l_2\rangle`，则
`PM+kMN\geqslant PM+kOM\sin\langle l_1,l_2\rangle=PM+OM\sin\langle l_1,l_3\rangle=PM+M` 到 `l_3` 的距离 `\geqslant P` 到 `l_3` 的距离。

hjfmhh

回复 10# kuing

Kuing书写好像错误了，Sin<l2,l3>应改为Sin<l1,l2>吧？

色k

回复 11# hjfmhh

嗯，打错了

游客

跟2楼和10楼是一个意思。
这个题宁波的高三模拟统考也考过，最后一个填空，是个平面几何题，很无语。

敬畏数学

怎么玩此题也应该玩得出。目测应该可以搞定。

敬畏数学

回复 1# realnumber
物理解法倒还挺有意思，哈！