请教一道几何问题

25717246

已知等边$\triangle ABC$中，点$M$满足：$\angle BMC=120^\circ$，则$\frac{MA}{MC}$的范围是_______.

kuing

又来玩玩速度分解（运动法）……

设 `\triangle ABC` 的中心为 `O`，其关于 `BC` 对称的点为 `O'`，则易知 `M` 的轨迹是弧 `BOC` 及弧 `BO'C`（不含端点），显然当 `M\to C` 时 `MA/MC\to\infty`，所以只需求最小值。

如果 `M` 在弧 `BO'C` 上，则将 `M` 对称到弧 `BOC` 上时 `MA` 更小；如果 `M` 在弧 `OC` 上，则将其对称到弧 `OB` 上时 `MC` 更大，这说明 `MA/MC` 取最小值时 `M` 必在弧 `OB` 上。

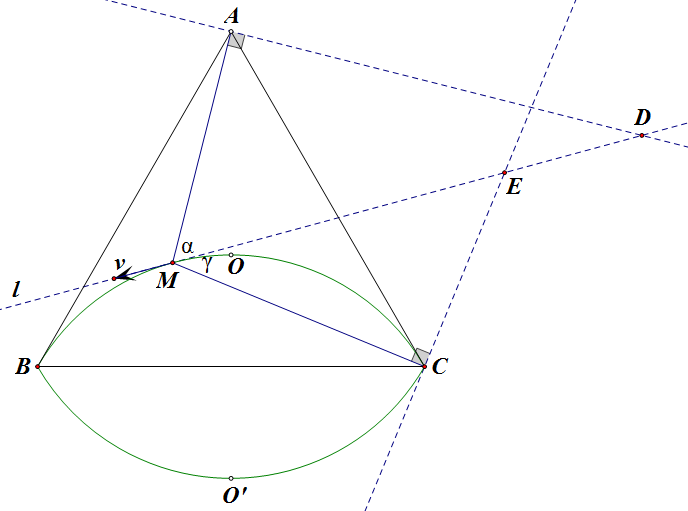
现在，让 `M` 自 `O` 向 `B` 运动，速度为 `v`，记 `M` 处的切线为 `l`，设 `MA`, `MC` 与 `l` 的夹角分别为 `\alpha`, `\gamma`，则
\begin{align*}
\frac{\rmd MA}{\rmd t}&=v\cos\alpha,\\
\frac{\rmd MC}{\rmd t}&=v\cos\gamma,
\end{align*}再分别过 `A`, `C` 作 `MA`, `MC` 的垂线与 `l` 分别交于 `D`, `E`，如上图，那么
\begin{align*}
\frac{\rmd}{\rmd t}\left( \frac{MA}{MC} \right)
&=\frac1{MC^2}\left( \frac{\rmd MA}{\rmd t}MC-\frac{\rmd MC}{\rmd t}MA \right)\\
&=\frac v{MC^2}(MC\cos\alpha-MA\cos\gamma)\\
&=\frac{v\cos\alpha\cos\gamma}{MC^2}\left( \frac{MC}{\cos\gamma}-\frac{MA}{\cos\alpha} \right)\\
&=\frac{v\cos\alpha\cos\gamma}{MC^2}(ME-MD), \qquad(*)
\end{align*}由此可见，`MA/MC` 取最小值时必定是当 `D`, `E` 重合时。

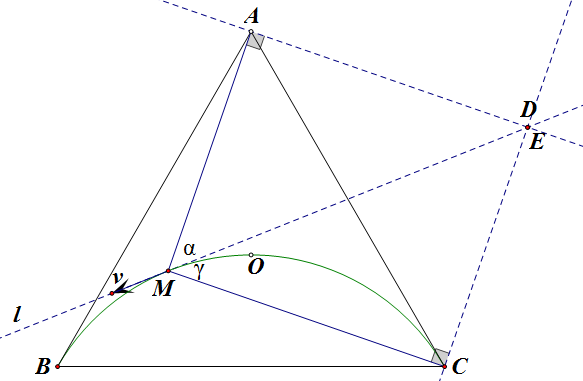
如图，当 `D`, `E` 重合时，则 `A`, `M`, `C`, `D` 四点共圆，由于 `AC` 也是弧的切线，故
\[\angle ACM=\gamma=\angle DAC,\]所以 $AD\px MC$，可见此时 `AMCD` 恰好是矩形！

至于此时怎么求 `MA/MC` 的值，且听下回分解……（其实就是还没想到秒杀的计算方法）

kuing

有了：

设 `\angle MCA=x`，则 `\angle MBC=x`，不妨设 `\triangle ABC` 边长为 `1`，则当 `MA\perp MC` 时，`MC=\cos x`，那么在 `\triangle MBC` 中使用正弦定理即得
\[
\frac{\cos x}{\sin x}=\frac1{\sin120\du}
\riff \frac{MA}{MC}=\tan x=\sin120\du=\frac{\sqrt3}2,
\]这就是最小值，所以所求范围就是 `\bigl[\sqrt3/2,+\infty\bigr)`。

这样就实现了极小计算量的解答

hejoseph

显然只需考虑 $M$ 在 $\triangle ABC$ 内部的情形，设 $\triangle ABC$ 边长为 1，$\angle MBC=\alpha$，则 $\angle MCB=60^\circ-\alpha$，$\angle MCA=\alpha$，其中 $0^\circ<\alpha<60^\circ$，由正弦定理得
\[
MC=\frac{\sin\alpha}{\sin 120^\circ}=\frac{2\sin\alpha}{\sqrt 3}，
\]
再由余弦定理得
\[
MA^2=1+MC^2-2\cdot MC\cos\alpha，
\]
所以
\[
\left(\frac{MA}{MC}\right)^2=\frac{1}{MC^2}+1-\frac{2\cos\alpha}{MC}=\frac{3}{4}\cot^2\alpha-\sqrt 3\cot\alpha+\frac{7}{4}，
\]
剩下的就是二次函数的问题了，不再写了。

kuing

噢，其实有了 3# 的方向，已经可以用很常规的方法来撸这道题了，也没什么难度。

继续沿用 3# 的图以及设边长为 `1`，有
\begin{align*}
MC&=\frac{\sin x}{\sin120\du}=\frac2{\sqrt3}\sin x,\\
MA^2&=1+MC^2-2MC\cos x,
\end{align*}所以
\begin{align*}
\frac{MA^2}{MC^2}
&=\frac1{MC^2}+1-\frac{2\cos x}{MC}\\
&=\frac3{4\sin^2x}+1-\frac{\sqrt3\cos x}{\sin x}\\
&=\frac34(1+\cot^2x)+1-\sqrt3\cot x\\
&=\frac34\left( \cot x-\frac2{\sqrt3} \right)^2+\frac34\\
&\geqslant\frac34,
\end{align*}
即 `MA/MC\geqslant\sqrt3/2`。

kuing

回复 4# hejoseph

我反应慢了几分钟……

isee

原来平几还比较难
我看正三角形，圆，又是距离比，就想上坐标系了，没细思了

kuing

值得一提的是，原题由于数据特殊，才导致取最值时 `MA\perp MC`，但是由速度分解得到的式 `(*)` 是具有一般性的，只要曲线是光滑的就可以这样玩儿。
因此，比如下图，`P` 是绿线上的动点，`A`, `B` 是定点，则当切线与两条垂线三线共点时，`PA/PB` 必处在稳定点（不一定是极值）

游客

用阿氏圆看看.

kuing

回复 9# 游客

所以就是要算一个与弧 BOC 相切的阿氏圆出来，像下面这样？：

游客

回复 10# kuing

是的，你画图比我快，这个能用待定系数法算（相切时），但不知道好不好算。

kuing

原来平几还比较难
我看正三角形，圆，又是距离比，就想上坐标系了，没细思了
isee 发表于 2019-4-8 12:05

话说，我试了一下建系，还真简单……

不妨设 `A(-1,0)`, `C(1,0)`, `B\bigl(0,\sqrt3\bigr)`，则不难计算出里面那段弧所在的圆方程为
\[(x-1)^2+y^2-\frac4{\sqrt3}y=0,\]于是
\[\frac{MA^2}{MC^2}=\frac{(x+1)^2+y^2}{(x-1)^2+y^2}=1+\frac xy\sqrt3,\]接下来随便弄都可以了……

游客

huing

回复 9# 游客
终于有人提到阿波罗尼斯圆了，这才是正解。
阿氏圆的定义：到两定点距离之比为定值的点的轨迹。
有关的定义：那两定点称为基点偶，以基点偶为对径点偶的圆称为基圆。阿氏圆与基点偶连线的两交点称为分点偶。
有用的性质：阿氏圆与基圆正交。这是因为按定义，分点偶与基点偶调和共轭。

图1

如图1，当内分点N从A~C滑动时，分比（NAC）扫遍$0-\infty$。
在分比较小时，阿氏圆与红色蚌形线相离，M点不存在，MA/MC无值;
分比至某个最小值m时阿氏圆与红色蚌形线相切，M点出现，MA/MC开始有取值;
分比超过m后，阿氏圆与红色蚌形线相交于两点直至退缩为点C.
所以MA/MC的范围即$[m,\infty)$，问题归结为求相切位置及对应的分比m.
由阿氏圆与基圆正交可知，基圆中心 D 与两圆交点 F 的连线是阿氏圆的一条切线;
由于 DC 与蚌形线相切，故 $DM_{in}$ 亦是蚌形线的切线;
可见基圆与蚌形线的交点 $M_{in}$ 正是 N 滑动过程中阿氏圆初触蚌形线的切点，$DM_{in}$ 为公切线。

图2

下面来求对应的分比m. 见图2
基圆交BC边于其中心 E，易知$\triangle BM_{in}C\sim\triangle EM_{in}A $, 所以$m=AE/BC=\sqrt3/2$.

敬畏数学

回复 9# 游客
接下来如何完成？

乌贼

如图：
\[ \dfrac{MA}{MC}\geqslant \dfrac{ME}{MC}=\dfrac{ME}{MD}=\dfrac{\sqrt{3}}{2} \]

取等条件当$ \angle AMC=90\du  $时即当$ M $为$ \triangle BCM $的外接圆与以$ AC $为直径的园的交点时（除$ C $点外）

kuing

回复 16# 乌贼

卧C！原来这个才才是正正路解法！

isee

回复 16# 乌贼

果然平几辅助线更佳，赞

同时亦是17楼的简化

kuing

在学习了今早这帖：forum.php?mod=redirect&goto=findpost& … =10737&pid=52947（2#）的解法后，想起了本帖，最小值可以这样解：
显然只需考虑 $M$ 在 $\triangle ABC$ 内部的情形，如下图：

延长 `AM` 交圆于 `N`，由于 `AC` 与圆相切，则 `\triangle AMC\sim\triangle ACN`，记圆半径为 `R`，所以
\[\frac{MA}{MC}=\frac{CA}{CN}\geqslant\frac{CA}{2R}=\frac{\sqrt3}2,\]
当 `CN` 为直径时取等。

isee

kuing 发表于 2023-4-19 16:07
在学习了今早这帖：forum.php?mod=redirect&goto=findpost&ptid=10737&p ...

也处理过类似的，源自知乎提问


题：等腰直角△ABC内一点 P，角 A 为直角，若 ∠BPC=135°，则 PA/PC 的最小值为____.

如图 ，作三角形 BPC 的外接圆 O，由题设条件，易得 AC (及 AB ）为圆 O 的切线，(即正方形ACOB)， 于是延长 AP 交圆 O 于点 D，连结 DC 则 $\angle ADC=\angle ACP$ ，从而 $\triangle ACP \sim\triangle ADC$ ，于是 \[\frac{PA}{PC}=\frac{AC}{DC}\geqslant\frac {AC}{2OC}=\frac 12.\]