9年级平几垂足三角形

realnumber

锐角三角形ABC三边上分别有三点DEF，为什么是垂足时，三角形DEF周长最小，几何画板试了下是这样.怎么证？

青青子衿

\begin{align*}
l({\color{blue}x})&=\big|D_1D_2\big|=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\\
&=\dfrac{2h\,|b-c|}{(b^2+h^2)(c^2+h^2)}\sqrt{h^2\left[\left(b+c\right){\color{blue}x}+\left(h^2-bc\right)\right]^2+\left[h^2\left(b+c\right)+\left(h^2-bc\right){\color{blue}x}\right]^2}\\
\end{align*}
\begin{align*}  
l_{\,\min}({\color{blue}0})&=\dfrac{2h\,|b-c|}{(b^2+h^2)(c^2+h^2)}\sqrt{h^2\left(h^2-bc\right)^2+\left[h^2\left(b+c\right)\right]^2}\\
&=\dfrac{2h\,|b-c|}{(b^2+h^2)(c^2+h^2)}\sqrt{h^2 (b^2 + h^2) (c^2 + h^2)}\\
&=\dfrac{2h^2\,|b-c|}{\sqrt{(h^2+b^2)(h^2+c^2)}\,}\\  
\end{align*}

《数学思维与方法 研究式教学 第2版》陈鼎兴
第153页

pep.com.cn/rjwk/gzsxsxkj/2012/sxkj9/sxkj9zh/2 … 20120724_1881660.htm

realnumber

不太明白
好象是2个问题了，目标是DEF周长最小，不是到固定一点距离最小

青青子衿

回复 3# realnumber
算了，我还是传图吧……

realnumber

先谢谢，现在就学习下

kuing

俺也来贴个长图

郝酒

回复 4# 青青子衿

兄台 这本书的电子版能否分享下，谢谢：）
alsmtyb@sina.com

isee

回复 1# realnumber

张景中的 新概念几何 啊，潇振刚 几何变换与几何证题 啊，几何瑰宝啊，等等基本随便翻开一本几何科谱，竞赛书，都有

realnumber

E'E"分别是E关于AB,AC的对称点，当三角形DEF周长最小时，DFE'E"四点共线.若DFE'E"不在一直线上，则可以找到更小的周长（具体如下：先固定EF，E'D+DF最小时，E'DF三点共线，同样DFE"也如此）
后面大概有些想法，再想清楚些，待续

乌贼

回复 6# kuing
学习后简化

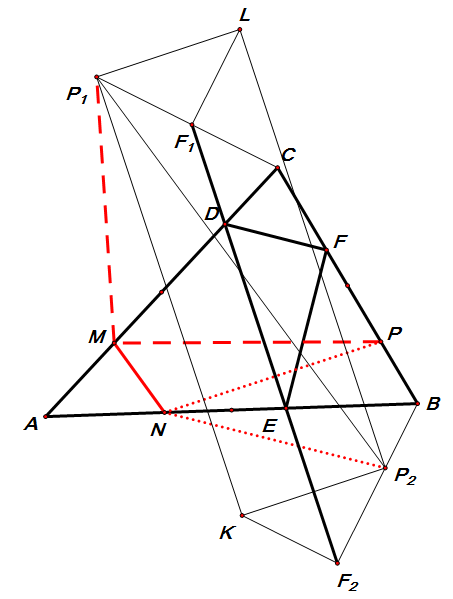
如上图：$ M,N,P $分别为$ AC,AB,BC $上任意一点，$ F,P $关于$ AC $的对称点分别为$ F_1P_1 $，$ F,P $关于$ AB $的对称点分别我$ F_2P_2 $，构造平行四边形$ P_1F_1F_2K $及平行四边形$ F_1F_2P_2L $
易知四边形$ P_1LP_2K $为矩形，有
  $ MN+NP+MP=MN+NP_2+MP_1\geqslant  P_1P_2$(取等条件：当点$ P_1,M,N,P_2 $共线时取得，见下图左)$\geqslant P_1K=F_1F_2$ （取等条件：点$ F $与点$ P $重合时取得见下图右）
   
综上$ MN+NP+MP\geqslant F_1F_2 $的取等条件为点$ F $与点$ P $重合(此时点$ F_1 $与点$ P _1$重合，点$ F_2 $与点$ P_2 $重合)且点$ P_1,M,N,P_2 $共线时取等（即点$ M $与点$ D $重合，点$ N $与点$ E $重合）见下图

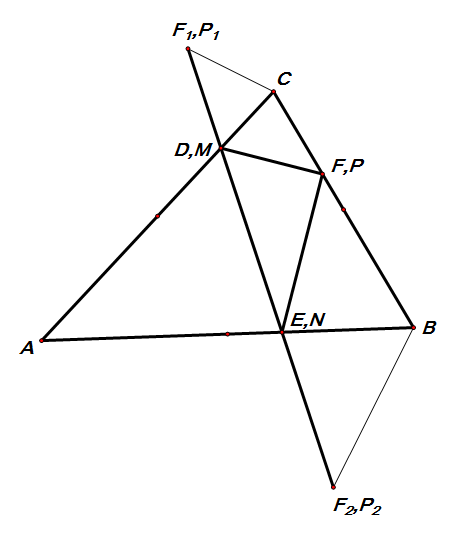
真不好表述