在有个角为$120$度的三角形中求高

isee

如图，在$\triangle ABC$中，$\angle BAC=120^\circ$，$AD\perp BC$，若$BD=\sqrt 3$，$DC=6\sqrt 3$，则$AD$=______.

中考模拟卷上的题目，我用面积法，三角形法，都可以求得$AD=2$，不过，平几何如何写呢？

isee

折腾了好久，得到一个十分复杂的辅助线。





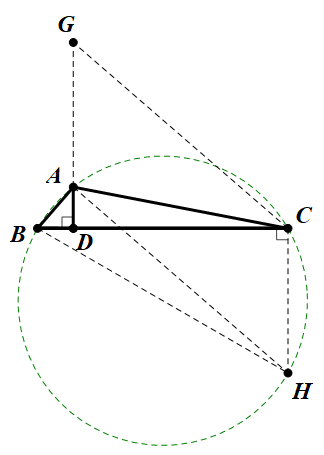
过点$C$作$BC$的垂线，交圆$ABC$于点$H$，连接$BH$，由$120$度角，容易得到$$CH=7,$$

再过点$C$作$CG$垂直于$BA$交$DA$的延长线于$G$，连接$AH$，则$AH$垂直于$BA$，从而有平行四边形$AHCG$，有$$GA=CH=7.$$

于是由$$\triangle GDC\sim \triangle BDA\Rightarrow AD=2.$$

乌贼

就是一道套路题呀，已知一定园及园上一定弦，求另一弦长。
\[ OC=2OF=2ED=\dfrac{FC}{\dfrac{\sqrt{3}}{2}}=\dfrac{7\dfrac{\sqrt{3}}{2}}{\dfrac{\sqrt{3}}{2}}=7 \\AE=\sqrt{AO^2-OE^2}=\sqrt{49-\dfrac{75}{4}}=\dfrac{11}{2}\\AD=AE-DE=\dfrac{11}{2}-\dfrac{7}{2}=2\]

isee

就是一道套路题呀，已知一定园及园上一定弦，求另一弦长。
\[ OC=2OF=2ED=\dfrac{FC}{\dfrac{\sqrt{3}}{2} ...
乌贼 发表于 2019-5-9 13:15

这么一看，果然呐，让我想起了，多好年前“海淀九年级期中卷”某一题。。

爪机专用

还真不了解这种套路……

PS、好久没登这个马甲了

isee

三角就是用和用正切和角公式

记$\angle BAD=\alpha$，则$\angle DAC=120^\circ-\alpha$，于是$$6=\frac {CD}{BD}=\frac{\tan(120^\circ-\alpha)}{\tan \alpha}\Rightarrow \tan \alpha=\frac 2{\sqrt 3}=\frac{AD}{\sqrt 3}\Rightarrow AD=2.$$

爪机专用

回复 6# isee

我的话会用余弦定理。

isee

回复 7# 爪机专用


大致说一下

kuing

回复 8# isee

这还用说吗……
设 `AD=x`，则 `BC^2=AB^2+AC^2+AB\cdot AC\iff147=x^2+3+x^2+108+\sqrt{(x^2+3)(x^2+108)}` 解得 `x=2`。

isee

回复 9# kuing

赞。（大拇指表情呢？）

果然是向量形式，不过，对初中生，这个可以改进一下，改成用勾股定理+面积建立方程求高。