一个函数问题

dding

设 $f[0,1]\to [0,1]$,且$f(x)$单调不减,满足以下两个条件
$$f(x)+f(1-x)=1$$
$$\dfrac{f(x)}{2}=f\left(\dfrac{x}{3}\right)$$
证明:对每个无理数$\alpha$, 存在唯一的$\beta$ 使得
$$f(\beta)=\alpha$$

色k

我只知道这个叫 Cantor 函数……

盗链个图看能不能显示：（显示不了，已删除）

色k

在百度百科 https://baike.baidu.com/item/康托尔函数/9994208 里看到该函数的另一种定义：

康托尔函数 c: [0,1] → [0,1] ，对于x∈[0,1]，其函数值c(x)可由以下步骤得到：

• 以三进制表示x。
• 如果x中有数字1，就将第一个1之后的所有数字换成0。
• 将所有数字2换成数字1。
• 以二进制读取转换之后的数，这个数即为c(x)。

从这种定义来看，1# 的命题是显然的。
若 `c(x)` 是无理数，那么 `x_3` 就不能有 1，故 `c(x)_2` 所有的 1 都是由 `x_3` 中的 2 变出来的，因此 `x` 是确定的。
（上述下标表示进制）

于是，我们现在要做的，就是证明这个定义与 1# 的定义是等价的即可。

isee

回复 2# 色k


盗链图果然不显。。

楼主这题，应该是竞赛级别的。。

色k

回复 4# isee

好吧，果然防盗链。无所谓了，就是 Cantor 函数的图象而已，随便搜一下也能找到……
当年人教论坛上还有人作过动图（没记错是 milksea），现在找不到了……

========================
原来 Mathematica 就有相应的函数 CantorStaircase。
用 Plot[CantorStaircase[x], {x, 0, 1}, PlotPoints -> 1000, AspectRatio -> 1] 即得：

战巡

回复 1# dding

还有一种定义是这样的
令$f_0(x)=x$，然后
\[f_{n+1}(x)=
\begin{cases}
\frac{1}{2}f_n(3x) & 0\le x\le \frac{1}{3} \\
\frac{1}{2} & \frac{1}{3}<x<\frac{2}{3} \\
\frac{1}{2}+\frac{1}{2}f_n(3x-2) & \frac{2}{3}\le x\le 1
\end{cases}
\]
然后$\lim_{n\to\infty}f_n(x)=f(x)$，之后可以证明康托函数在$[0,1]$上是连续的

realnumber

1楼x=0,1代入很奇怪，得到
f(0)-f(1)=1=f(1)-f(0)

kuing

回复 7# realnumber

你看错符号了。

kuing

回复 6# 战巡

学习鸟，来个动图演示 `f_n(x)` 的变化：

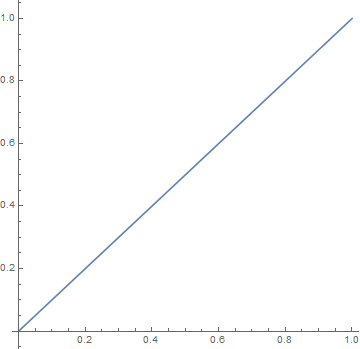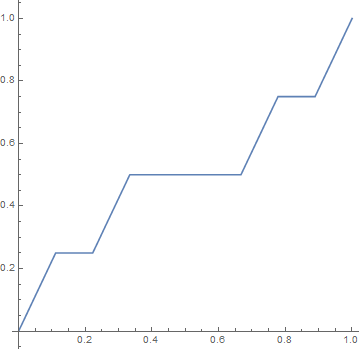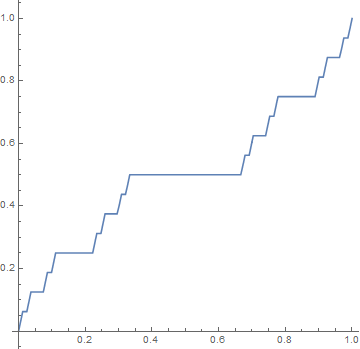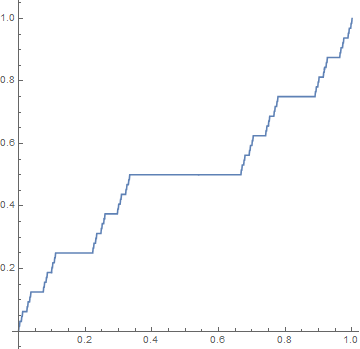
生成此图的 MMC(A) 代码：

1. f[0, x_] = x;
2. f[n_, x_] := 0.5 f[n - 1, 3 x] /; 0 <= x <= 1/3;
3. f[n_, x_] := 0.5 /; 1/3 < x < 2/3;
4. f[n_, x_] := 0.5 + 0.5 f[n - 1, 3 x - 2] /; 2/3 <= x <= 1;
5. test = Table[Plot[f[k, x], {x, 0, 1}, PlotPoints -> 10*2^k, AspectRatio -> 1], {k, 0, 6}];
6. Export["test.gif", test]

Copy the Code

然后在我的文档里找 test.gif ，用其他工具编辑一下时间即得。

hbghlyj

搞懂Cantor（康托）集
相关帖子
forum.php?mod=viewthread&tid=9519
forum.php?mod=viewthread&tid=8999