求一向量表达式最小值

realnumber

\[ \abs{\vv{a}}=\abs{\vv{b}}=\abs{\vv{c}}= 1,\vv{a}\cdot \vv{b}=0  \]
求$\abs{0.5\vv{c}-\vv{a}}+\abs{2\vv{c}-\vv{b}}  $的最小值.

facebooker

7彩阳光联盟的题目
就是根据对称性|0.5c-a|=|c-0.5a| 这样转化一下

色k

\[
\abs{0.5\bm c-\bm a}+\abs{2\bm c-\bm b}
=\abs{\bm c-0.5\bm a}+\abs{\bm c-2\bm b}
\geqslant\abs{0.5\bm a-2\bm b}=\frac{\sqrt{17}}2,
\]取等略。

色k

码代码慢了一分钟

敬畏数学

不妨设$\vv{c}=(1，0)，\vv{a}=(cos\theta ，sin\theta )，\vv{b}=(-sin\theta ，cos\theta )，\theta ∈[0，2π]$，则$ |\frac{1}{2}\vv{c}-\vv{a}|+ |2\vv{c}-\vv{b}|=\sqrt{(cos\theta -\frac{1}{2})^2+(sin\theta -0)^2} +\sqrt{(cos\theta -0)^2+(sin\theta -(-2))^2}$，表示单位圆上的点到$ （\frac{1}{2}，0），（0，-2） $距离之和的最小值，显然$ \sqrt{\frac{1}{4}+4}=\frac{\sqrt{17}}{2} $，等号取得满足：$ cos\theta =\frac{1}{\sqrt{17}}，sin\theta =-\frac{4}{\sqrt{17}} $。

爪机专用

回复 5# 敬畏数学

题目没说它们是平面向量。

乌贼

回复 5# 敬畏数学
回复 6# 爪机专用

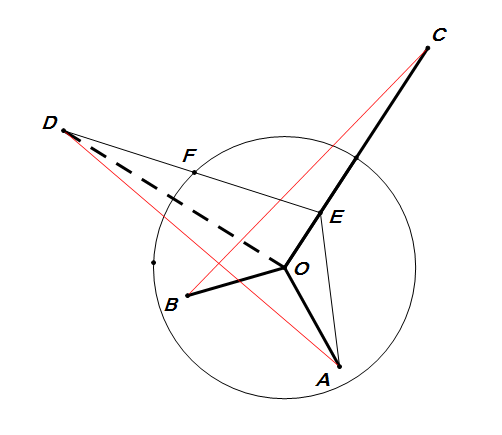
那就把它变空间向量，球$ O $半径为1，$ A,B $为球面上两点且$ AO\perp BO $，$ CO=2 $，点$ E $在$ CO $上且$ OE=\dfrac{1}{2} $，作$ DO=CO,DO\perp CO,\angle AOD=\angle COB $，$ F $为$ DE $与球面交点。有\[ \triangle AOD\cong \triangle COB\riff AD=CB \]所以$ CB+AE=AD+CE\geqslant DE=\dfrac{\sqrt{17}}{2} $（取等条件点$ A,F $重合时）

敬畏数学

大师！学习。。。。。。辛苦啦。

走走看看

回复 5# 敬畏数学

如果这是平面向量，设的坐标很巧妙，否则不能转换成线段和。