一个向量数量积的最值

力工

在做题时遇到：已知 椭圆$\dfrac{x^2}{4}+\frac{y^2}{3}=1$上的动点$P$，
圆$(x-1)^2+y^2=16$上的动点$Q$，且$F(-1,0)$，求$\vv{FP}\cdot \vv{FQ}$
的取值范围.
坐标代入后，可得
$2(2cos\theta +1)(2cos\varphi +1)+4\sqrt{3}sin\theta sin\varphi $，但后面
算不下去了。求助高招。

kuing

既然那个点是焦点，那就从几何角度考虑呗……

最大值太简单，显然 `FP\leqslant 3`, `FQ\leqslant 6`，所以 $\vv{FP}\cdot\vv{FQ}\leqslant FP\cdot FQ\leqslant18$，当 `P(2,0)`, `Q(5,0)` 取等；

至于最小值，设圆心为 `G`，则 $\vv{FP}\cdot\vv{FQ}$ 取最小值时必然 $\vv{FP}\px\vv{GQ}$ 且方向相反，如下图所示，即 $\vv{FP}\cdot\vv{FQ}\geqslant-FP\cdot HQ$。

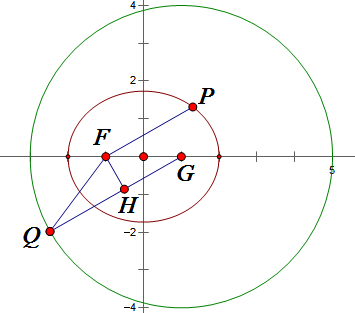
记 `\angle PFG=\theta`，根据圆锥曲线极坐标公式，易知 `FP=3/(2-\cos\theta)`，而由 $FP\px GQ$ 易得 `HQ=4-2\cos\theta`，从而 `FP\cdot HQ` 恒为 `6`，可见 $\vv{FP}\cdot\vv{FQ}$ 的最小值就是 `-6`。

综上，由连续性即得取值范围就是 `[-6,18]`。

敬畏数学

双动点，先固定椭圆上的点，显然与圆心一直线上，同向共线为最大，反向共线为最小。$ \vv{FQ}=\vv{FG}+\vv{GQ} $

力工

回复 2# kuing

回复 3# 敬畏数学

谢谢！某渣已硬算解决！