根据分段函数的复合函数的零点数求参数范围

走走看看

1、已知函数$g(x)=-x+1(x＜0），g(x)=x^2-1(x≥0)，若函数y=g(g(x))-2m$有三个不同的零点，则实数a的取值范围。
答案：$(\frac{1}{2},1]$，无解析。

2、已知函数$f(x)=-x+m(x＜0），f(x)=x^2-1(x≥0)，其中m＞0，若函数y=f(f(x))-1$有三个不同的零点，则m的取值范围。
答案：(0,1)，有解析。
zybang.com/question/b2a17ff8f202a6657991f89b8cab93a7.html

附注：

1题，按照画图的方式，知道2m＞1，但只得到了$m＞\frac{1}{2}$，那个1得不出来。

2题，用分类讨论法，但总感到这个上面链接所给的解答过程有问题。
第一个分类，没有省去解；第二、第三个分类，有意省去了一个解。难道做题可以
自作主张，想怎么做就怎么做吗？前面给定的x，与后面解出的x有无约束关系？

这两题如果只画图是否也可以得到答案呢？
请大师们赐教！

走走看看

回复 1# 走走看看

昨天的那道题，是一个函数的复合，这里是分段函数的复合。
只知道，2m这条直线与g(g(x))的图象的交点的横坐标要满足x1∈[-1,1]，x2∈(1,+∞)。

走走看看

回复 1# 走走看看

第1题的解答：
x1<x2，
-1≤x1<0  ，x1=1-2m，解得$\frac{1}{2}＜ m≤1$
x2>1,$\sqrt{1+2m}>1$，解得 m＞0。
所以$m∈ (\frac{1}{2},1]$。


粗红线是 分段函数的复合函数图象，细红线是直线y=2m，蓝线是原分段函数。

第2题也可以这样图解。
顺便说，这与昨天的复合函数没有本质区别。这是在K大师昨天的点拨下才实现的简便方式。
这里是把那种解法平行移动过来的。

走走看看

网络上的解析可能是正确的，因为在小猿搜题上也配备了视频讲解。
那里的文字解析正是如此。

另外，感到前面的x范围，应该不影响后面的x的范围。

力工

回复 3# 走走看看
不知高人的那个粗红线（复合函数的图象）是如何作出来的。请赐教。

isee

回复 5# 力工

我认为楼主是手动绘的。即手动分段绘的。几何画板也能绘f(g(x))，也能自定义定义域。 扩展用符号函数1，另个参考符号函数2

分段函数之类，还是用GGB之类的吧，有原生命令（代码），。

走走看看

我的笔记本网卡今天上午出了问题，系统检测不到，现在是手机上网。我是几何画版画的，非手工画的。等到笔记本能上网时，我上传一下第一题的画板文件。

爪机专用

回复 6# isee

上次还画过分段+周期 forum.php?mod=viewthread&tid=5947

走走看看

回复 5# 力工

分段函数的复合函数的参数取值范围1.gsp (3.66 KB, Downloads: 3446)

2019-6-3 20:56 Upload

Click on the file to download the attachment

网购了一个无线网卡，下午刚到。

hbghlyj

isee 发表于 2019-5-31 03:17
回复 5# 力工
我认为楼主是手动绘的。即手动分段绘的。几何画板也能绘f(g(x))，也能自定义定义域。 扩展 ...

几何画板中函数和分段函数定义域处理

郑 明 淮

(福建尤溪文公高级中学，365100)

几何画板是数学新课程推荐使用信息技术软件。它作出的几何图形、函数图象非常精确，运算功能也十分强大，更重要的是它拥有用动态方式揭示几何图形中的元素间关系保持不变的特点。这些特点对于学生认清问题的本质，弥补空间想像力不足，对相关问题进行验证、探索提供了易于操作的平台。正因为如此，几何画板相对于其他常用软件倍受数学教师的青睐。

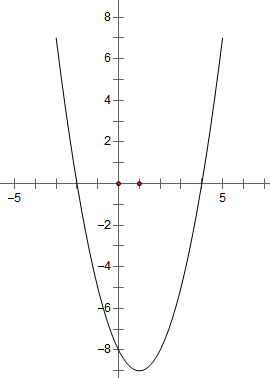
当然，任何一款软件都不可能做到十全十美，几何画板也是如此。虽然它的版本已经升级到5.0，我们在使用过程中仍然发现有许多方面不尽如人意。例如：新建一个函数后，利用绘制函数图象功能画出来的是其完整定义域上的图象。而在高中数学中很多函数是限定定义域的，而几何画板不具备直接限定定义域的作图像功能，我们只能另想方法以达到这一目的。这一问题以及分段函数是高中数学中的重点内容，在使用几何画板辅助教学中必需突破这一瓶颈。本文就此两个问题在几何画板环境下做一个探索，希望能有效地、可操作地解决这一问题。

一、几何画板中限定定义域函数的图像处理方案

例1、作函数$y=x^{2}-2 x-8$($-3 \leq x \leq 5$)的图像

分析：$y=x^{2}-2 x-8$的定义域是R，要去掉$-3 \leq x \leq 5$之外的图像只能改变原函数的表达式，使其对应关系与原函数相同，但定义域为$-3 \leq x \leq 5$。构造如下： $f(x)=x^{2}-2 x-8+0 \cdot \sqrt{(x+3)(5-x)}$然后绘制函数f(x) 效果如图。

函数f(x) 中的$0 \cdot \sqrt{(x+3)(5-x)}$把函数定义域限定在$-3 \leq x \leq 5$，并且在定义域范围内其值恒为0，因此不改变原函数的值。

一般地，限定函数定义域的构造有以下八种情况：

1、限定函数f(x)定义域为[a，b]构造函数：$y=f(x)+0 \cdot \sqrt{(x-a)(b-x)}$

2、限定函数f(x)定义域为(a，b]构造函数：$y=f(x)+0 \cdot \sqrt{\frac{b-x}{x-a}}$

3、限定函数f(x)定义域为[a，b)构造函数：$y=f(x)+0 \cdot \sqrt{\frac{x-a}{b-x}}$

4、限定函数f(x)定义域为(a，b)构造函数：$y=f(x)+0 \cdot \log ((x-a)(b-x))$

5、限定函数f(x)定义域为(a，+∞)构造函数：$y=f(x)+0 \cdot \log (x-a)$

6、限定函数f(x)定义域为[a，+∞)构造函数：$y=f(x)+0 \cdot \sqrt{x-a}$

7、限定函数f(x)定义域为(-∞，b)构造函数：$y=f(x)+0 \cdot \log (b-x)$

8、限定函数f(x)定义域为(-∞，b]构造函数：$y=f(x)+0 \cdot \sqrt{b-x}$

二、几何画板中分段函数的图像处理

例2．作分段函数$f(x)=\left\{\begin{array}{l}3 x+8 \ldots \ldots \ldots .(x<-2) \\ x^{2} \ldots \ldots \ldots \ldots \ldots(-2 \leq x<4) \\ -3 x+6 \ldots \ldots \ldots(x \geq 4)\end{array}\right.$的图像。

在网络上或下载的课件中经常看到的两种作法：

方法1：分别构造函数

①$f_{1}(x)=3 x+8+0 \cdot \log (-2-x)$

②$f_{2}(x)=x^{2}+0 \cdot \sqrt{\frac{x+2}{4-x}}$

③$f_{3}(x)=-3 x+6+0 \cdot \sqrt{x-4}$

这里对三个函数的定义域分别作出了限制，然后分别绘制这三个函数的图象。这一方法虽然可以在屏幕上同时显示出了f(x)函数图像，但本质上它是三个不同函数的图像，只是在视觉上让学生感觉是分段函数的图像。若要对分段函数作进一步的研究，如：在f(x)定义域内任取x 的值计算其函数值则只能人工判断用哪个式子进行了。若要动态显示f(x)整个变化过程则显然无能为力。因此这种做法的缺陷是明显的。

分段函数本意上是一个函数，定义域是各段函数定义域的并集，只是在每一段内其对应关系不同。

在画板作图中应要求：1、函数图象能一次性作出。2、在选择函数图象时，能整体选中。3、在图象上任取一点，这一点应该能在各段图像上自由的移动。这才是几何画板中的真正意义上分段函数。

方法2：首先定义函数①$f_{1}(x)=3 x+8$，②$f_{2}(x)=x^{2}$，③$f_{3}(x)=-3 x+6$

然后构造函数：$g(x)=\frac{1+\operatorname{sgn}(-2-x)}{2} f_{1}(x)+\frac{\operatorname{sgn}(x+2)+\operatorname{sgn}(4-x)}{2} f_{2}(x)+\frac{1+\operatorname{sgn}(x-4)}{2} f_{3}(x)$

绘制g(x)的图像。

这一做法的结果是在画面上g(x)的图像与f(x)的图像完全相同，并且满足上面所说的三个基本要求。因此这一构造法成为经典被列入几何画板常用自定义工具中。实际上，这种构造仍然只是障眼法。它根本上忽视了分段点的归属。我们分析g(x)中的三个构造的式子$\frac{1+\operatorname{sgn}(-2-x)}{2}$、$\operatorname{sgn}(x+2)+\operatorname{sgn}(4-x)$和$\frac{1+\operatorname{sgn}(x-4)}{2}$，其原理是在它所匹配各段函数定义域范围内取值为1，其它范围内取值为0，在非分段点g(x)与f(x)的值完全相同。现考察其在分段点处的情形，当x= -2时它们的值分别为0.5、0.5和0，$g(-2)=0.5 f_{1}(-2)+0.5 f_{2}(-2)=3$，而$f(-2)=4$，显然f(-2)≠g(-2)；在x=4时，三个式子的值分别为0、0.5和0.5，$g(4)=5$ 而 $f(4)=-6$，同样$f(4) \neq g(4)$。这说明g(x)与f(x)并不是相同的函数。那么为什么从图像上看不出来呢，原因是几何画板存在这样的bug，函数图像中单个点的不会被显示。这一点也许是人们没有意识到或是有意加以利用。若没有这个bug，且函数的图像在分段处不连续，那必然在分段处出现一个孤立点。

那么，如何在几何画板中实现真正意义上的分段函数呢？下面给出我的方法，步骤如下：

(1)定义函数①$f_{1}(x)=3 x+8$，②$f_{2}(x)=x^{2}$，③$f_{3}(x)=-3 x+6$

(2)构造三个函数作为各段的选择因子：

k₁(x)=sgn(1+sgn(-2-x))*sgn(abs(-2-x)) 该函数只有当x＜-2时值为1，其余为0。

k₂(x)=sgn(1+sgn((x+2)(4-x)))*sgn(abs(4-x)) 该函数只有当-2≤x＜4时值为1，其作为0。

k₃(x)=sgn(1+sgn(x-4)) 该函数只有当x≥4时值为1，其余为0。

(3)构造g(x)=k₁(x)*f₁(x)+k₂(x)*f₂(x)+k₃(x)*f₃(x)

(4)选中函数g(x)，绘制函数即得f(x)的图像。

分析这一方法的基本原理：若一个含有n段的分段函数f(x)中，函数$f_{i}(x)$(i=1、2、…、n)的原始定义域的交集与f(x)的定义域相同，则针对$f_{i}(x)$自变量x限定范围内，构造相应的选择因子$k_{i}(x)$，其中$k_{i}(x)$(i=1，2，…，n) 的取值只为0或1，而且这n个中只能有一个为1。再构造函数$g(x)=\sum_{i=1}^{n} k_{i}(x) f_{i}(x)$则g(x)与f(x)是相同的函数。

一般地，利用画板中的sgn( )和abs( )函数可以构造八个不同类型的选择因子函数。根据分段函数中各段限定定义域的模型选择相匹配的选择因子函数，构造$g(x)=\sum_{i=1}^{n} k_{i}(x) f_{i}(x)$便可达到要求。具体的$k_{i}(x)$根据$f_{i}(x)$自变量x限定形式分别作如下构造：

1、 当x≤a 时选中：$k_{i}(x)$ =sgn(1+sgn(a-x))

2、 当x<a时选中：$k_{i}(x)$ =sgn(1+sgn(a-x))*sgn(abs(a-x))

3、 当x≥a 时选中：$k_{i}(x)$ =sgn(1+sgn(x-a))

4、 当x>a时选中：$k_{i}(x)$ =sgn(1+sgn(x-a))*sgn(abs(x-a))

5、 当a≤x≤b时选中：$k_{i}(x)$ =sgn(1+sgn((x-a)(b-x)))

6、 当a<x≤b时选中：$k_{i}(x)$ =sgn(1+sgn((x-a)(b-x)))*sgn(abs(x-a))

7、 当a≤x<b时选中：$k_{i}(x)$ =sgn(1+sgn((x-a)(b-x)))*sgn(abs(b-x))

8、 当a<x<b时选中：$k_{i}(x)$ =sgn(1+sgn((x-a)(b-x)))*sgn(abs((x-a)(b-x)))

对于$f_{i}(x)$中原始定义域交集与f(x)的定义域不同的问题中，直接按上述方法可能得不到$g(x)=\sum_{i=1}^{n} k_{i}(x) f_{i}(x)$的图象，因为g(x)的定义域就是$f_{i}(x)$(i=1、2、…、n)限定定义域的交集。在此情况下所构造的g(x)是无意义的。例如：$f(x)=\left\{\begin{array}{l}0 \ldots \ldots \ldots \ldots \ldots \ldots .(x<0) \\ \sqrt{x(1-x)} \ldots \ldots \ldots(0 \leq x \leq 1) \\ \ln (x-1) \ldots \ldots \ldots .(x>1)\end{array}\right.$此时按上面方法构造的g(x)定义域为φ。要解决这一问题可以用画板提供的取绝对值函数abs( )对$f_{i}(x)$的原始定义域进行扩展。本例中，$f_{1}(x)=0$，$f_{2}(x)=\sqrt{x(1-x)}$，$f_{3}(x)=\ln (x-1)$，三个函数的定义域交集为φ，f(x)定义域为R，可将$f_{2}(x)$和$f_{3}(x)$改写为下列方式把定义域扩展。

$f_{2}(x)=\sqrt{a b s(x(1-x))}$，$f_{3}(x)=\ln (a b s(x-\operatorname{sgn}(a b s(x-1))))$

其中$f_{3}(x)$中把1改为sgn(abs(x-1))的目的是把原来x=1时ln(x-1)无意义变为有意义。再构造选择因子函数：

$k_{1}(x)=\operatorname{sgn}(1+\operatorname{sgn}(-x))^{*} \operatorname{sgn}(a b s(x))$

$k_{2}(x)=\operatorname{sgn}(1+\operatorname{sgn}(x *(1-x)))$

$k_{3}(x)=\operatorname{sgn}(1+\operatorname{sgn}(x-1))^{*} \operatorname{sgn}(a b s(x-1))$

由于$k_{i}(x)$的特性，扩展部分的相应$f_{2}(x)$和$f_{3}(x)$函数值为0。在此基础上构造$g(x)=k_{1}(x)^{*} f_{1}(x)+k_{2}(x)^{*} f_{2}(x)+k_{3}(x)^{*} f_{3}(x)$与$f(x)$是等价的。函数图象如图所示。

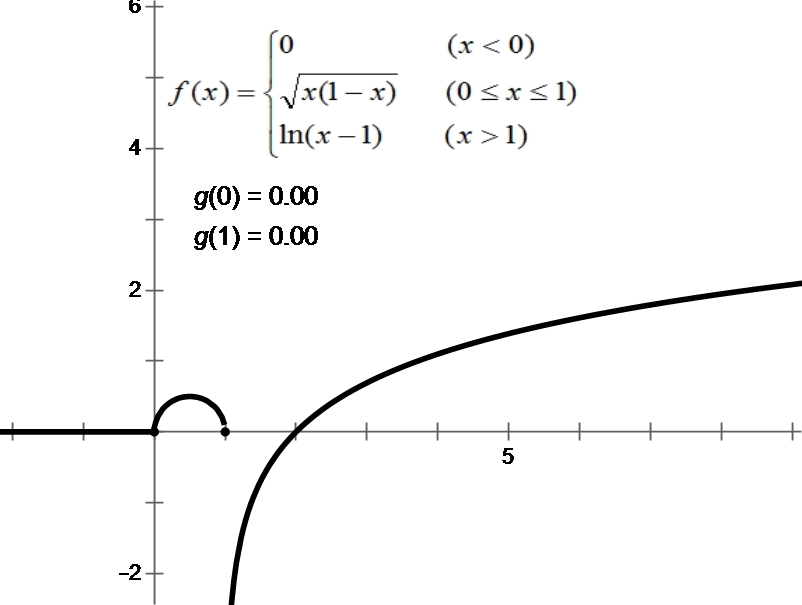几何画板的分段函数的问题，历来是喜欢用画板的老师热议的问题，各种创造性的发挥还将层出不穷。本文所提及的解决方法也许只是其中的一小部分，还脱离不了实际操作层面的繁琐。建议将限定定义域的8种类型和分段函数8种选择因子函数做成自定义工具，这样在实际使用中会方便一些。