一道平面几何题感觉做繁了太多

hbghlyj

∠C=90°,∠CED=∠BED=30°,AC=14,BE=3$\sqrt{21}$,求AE

作图中的遇到一个巧合，不知是何缘故：以A为圆心过E的圆和BCE的外接圆的另一交点在AB上

乌贼

$\triangle EFB$为等边三角形，$\dfrac{CD}{DQ}=\dfrac{14}{\dfrac{3\sqrt{21}}{2}}=\dfrac{4\sqrt{21}}{9}$

hbghlyj

回复 2# 乌贼
我也想到作等边三角形，ACBQ共圆等等。这样能把方程简化一些。
我觉得题目给的数据就是一个巧合。换个数就是层层根号了。

isee

回复 1# hbghlyj

我的解法与楼主的法2相同，不过，这个高次方程是如何解的？$$\frac {81\times 7}{4(x^2+9\sqrt{7}x-7)}+\frac{x^2}{28^2}=1.$$

isee

回复 2# 乌贼


然后怎么办？

hbghlyj

回复 5# isee
令x=√7t，这样就能把系数都变成有理数，然后用有理根定理。

乌贼

回复 5# isee

然后：正$ \triangle ABC,AB=a $，$ D $为$ BC $中点，$ F $在$ AB $上，$ FE=KDE,BG\px AD $交$ CF $延长线于$ G $。
令$ DE=x $。有\[ \triangle BGF\sim \triangle AEF\riff\dfrac{GF}{EF}=\dfrac{BG}{AE} \riff\dfrac{\sqrt{\dfrac{a^2}{4}+x^2}}{Kx}-1=\dfrac{2x}{\dfrac{\sqrt{3}a}{2}-x}\\\riff K=\dfrac{(\dfrac{\sqrt{3}a}{2}-x)\sqrt{\dfrac{a^2}{4}+x^2}}{(\dfrac{\sqrt{3}a}{2}+x)x}\]回到原题易知$K=\dfrac{28}{3\sqrt{21}}$，然后各种数字运算……求$ x $

isee

回复 7# 乌贼


    这依然是个四次方程，看来此题很刁

乌贼

回复 8# isee
已知$ x $求$ K $就不刁了

hbghlyj

回复 9# 乌贼
1#的意思是这题的数据是一个巧合，因此可能有更简单的办法.我另作了下图，将AC：BE调整了一点，发现以A为圆心过E的圆和BCE的外接圆的另一交点就不在AB上了.进而发现没有其他位置满足这个条件，AE重合的情形除外.再明确一遍,这题的数据是一个巧合,因此可能利用数据,构造图形,利用这个巧合,得到更简单的办法.

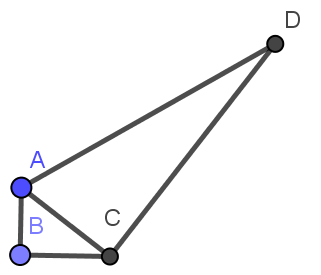
我们另举一经典几何题为例:已知凸四边形ABCD的各边和一角,求较长的对角线的长度.这个题需用余弦定理算出给定角所对的对角线,再算它和其他边成的角,再用余弦定理求出第二条对角线，然后再比较.
但是我们给出数据AB=3,BC=4,CD=12,DA=13,∠B=90°，这道题轰然塌缩成初中填空题：我们利用数据的巧合，连接AC（上面所说的构造图形），由勾股定理，AC=5，由勾股逆定理，∠ACD=90°（上面所说的利用数据的巧合），然后由D作BC垂线DH,利用相似求出$CH=\frac{36}5,DH=\frac{48}5$再由勾股定理即可求出$BD=\frac85\sqrt{85}$

以上是我个人的见解,希望见到简单的办法