|
|
Last edited by hbghlyj 2024-5-17 11:44X,Y都是复数构成的集合,现在定义它们的积为$XY:=\{xy|x\in X,y\in Y\}$,求下面各图形对应的复数集合的积表示的区域
Ⅰ直线、直线
Ⅱ直线、圆
Ⅲ圆、圆。大概是心脏线或者蜗线吧
(这里的"圆"都不包含内部)
下图是两条不过原点的直线之积
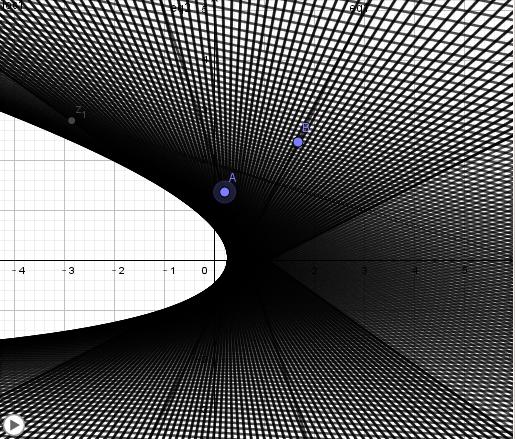
两条不过原点的斜率相反的直线之积
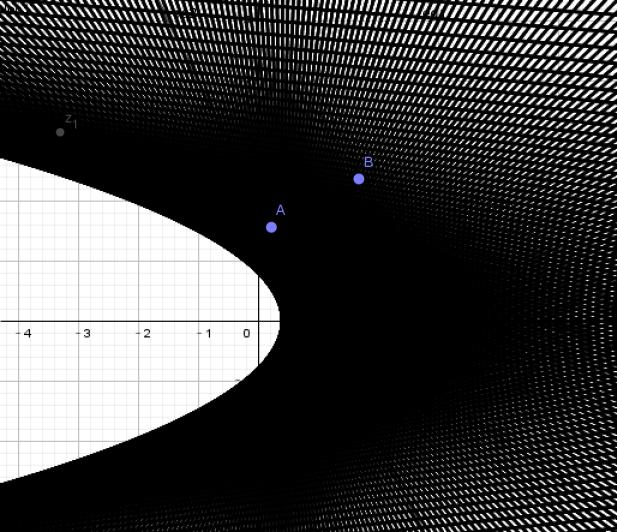
两条不过原点的直线之积是抛物线的外部,且区域内每个点都是二重点.当且仅当斜率相反时,抛物线的对称轴为x轴.
证明:设两条直线倾斜角为$\theta,\phi$,与x轴的交点为a,b.$\lambda,\mu$是实参数.
由$x=a b+a \mu \cos \phi+b \lambda \cos\theta+\lambda \mu \cos(\theta+\phi),y=a \mu \sin \phi+b \lambda \sin\theta+\lambda \mu \sin(\theta+\phi)$消去$\mu$得一个关于$\lambda$的二次方程:
\[-a^2 b \sin \phi-2 a b \lambda \cos\theta \sin \phi+a x \sin \phi-b \lambda ^2 \sin ^2\theta \sin \phi-b \lambda ^2 \cos ^2\theta \sin \phi+\lambda x \sin\theta \cos \phi+\lambda x \cos\theta \sin \phi=y (a \cos \phi-\lambda \sin\theta \sin \phi+\lambda \cos\theta \cos \phi)\]
令$\Delta\ge0$得\[-4 a^2 b^2 \sin ^2(\theta ) \sin ^2(\phi )+a b x (\cos (2 \theta +2 \phi )-\cos (2 \theta )-\cos (2 \phi )+1)+a b y (\sin (2 \theta +2 \phi )-\sin (2 \theta )-\sin (2 \phi ))+x^2 \sin ^2(\theta +\phi )-x y \sin (2 \theta +2 \phi )+y^2 \cos ^2(\theta +\phi )\ge0\]表示一个倾斜角为$\theta+\phi$的抛物线的外部 |
|