圆锥曲线的焦点三角形几心问题

敬畏数学

椭圆、双曲线焦点三角形的内心、外心、重心、垂心、旁心的轨迹分别是什么？有这方面的结论吗？

kuing

先讲旁心和内心，因为都是搞过的。

椭圆的，左右旁心 `x=\pm a` 不用多说。

至于第三个旁心以及内心，我在《数学空间》2013 年第 2 期（总第 12 期）的《对《ab1962 解题集精选（十二）》里的一道椭圆题的拓展》一文中都推导过，结论是 `x^2+\frac{1-e}{1+e}y^2=c^2` 以及 `x^2+\frac{1+e}{1-e}y^2=c^2`。

文中最后我还说双曲线的结论类似啊限于篇幅不再详写啊留作练习，其实就是懒得码字，不过查回《撸题集》发现我在 2010 年初就推导过双曲线的左右旁心，见 P.883 题目 6.6.14，结论写成类似以上形式就是 `x^2-\frac{e+1}{e-1}y^2=c^2`，和椭圆的内心一样。

至于双曲线的第三个旁心以及内心也是简单的 `x=\pm a`，因此内心和旁心就都搞完了。

然后，外心、重心都是极简单的，外心当然就是 `y` 轴，重心就是将原曲线按比例缩小至 `1/3`。

所以剩下就是垂心还没搞。

kuing

垂心的推导也是简单的：

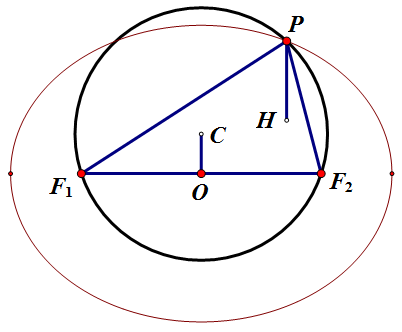
如图，外心 `C`，垂心 `H`，熟知有 $\vv{PH}=-2\vv{OC}$。

设 `P(x_0,y_0)`, `C(0,m)`，则 `x_0^2+(y_0-m)^2=m^2+c^2`，得
\[m=\frac{x_0^2+y_0^2-c^2}{2y_0},\]从而点 `H` 的纵坐标为
\[y_H=y_0-2m=\frac{c^2-x_0^2}{y_0},\]对于椭圆的情形，有 `y_0=\pm\frac ba\sqrt{a^2-x_0^2}`，由此可见垂心 `H` 的轨迹方程就是
\[y=\pm\frac ab\cdot\frac{c^2-x^2}{\sqrt{a^2-x^2}};\]对于双曲线的情形，有 `y_0=\pm\frac ba\sqrt{x_0^2-a^2}`，由此可见垂心 `H` 的轨迹方程就是
\[y=\pm\frac ab\cdot\frac{c^2-x^2}{\sqrt{x^2-a^2}}.\]