AB+CD⩽4PQ

hbghlyj

凸四边形ABCD对角线交于点O，P,Q为△ABO和△CDO的外心，求证：AB+CD⩽4PQ
原网页这个人显然是做错了。题目没说两圆外切，所以$PQ\leq r_1+r_2$，不等号方向怼了

kuing

看不到题，我这里进入那网页会跳转到登录界面，麻烦把题目码一下或截图上来。

kuing

在《撸题集》搜索 4PQ 发现你说的应该是 P.197 题目 2.2.12：
凸四边形 ABCD 的两条对角线相交于点 O，△ABO 和 △CDO 的外接圆圆心分别为点 P 和点 Q，求证：AB + CD ⩽ 4PQ。

hbghlyj

回复 3# kuing
哦。找到了。2015年版P197。
研究一下纯几何证法。方向是用解析法导出一些形式简单的结论，用纯几何证，再把这些结论连接起来。
还可研究一下内心连线、旁心连线、重心连线、垂心连线、九点圆圆心连线、类似重心连线、外类似中心连线、热尔岗点连线、奈格尔点连线、费马点（正等角中心）连线、负等角中心连线、斯俾克点连线、旁斯俾克点连线……与AB+CD比值的取值范围，这个话题可以延续几天了

hbghlyj

从pdf直接复制出来为什么是CMMI10、CMSY10、CMR7这种字体呢
还有，上标会复制成下标
有没有直接复制出来的办法呢
还有，这个\bullet在word中为什么显示不出来呢？
代码是
$A{{B}^{2}}+2(OA\bullet OC+OB\bullet OD)={{(rd-a)}^{2}}+{{r}^{2}}+2ac+2r({{d}^{2}}+1)$
切换了好几次都显示不出来呢？后面那个\bullet却能显示出来。{:sigh:}

加一个换行就好了。删掉换行就回去了

kuing

回复 5# hbghlyj

我 3# 的内容就是直接从 PDF 复制出来的，可能跟阅读器有关？（我用 SumatraPDF）

至于 word 的问题我不了解……

你是在把我那证明转录到你的文档上吗？

hbghlyj

回复 6# kuing
已经安装SumatraPDF并解决了直接复制的问题。感谢！
word的问题我觉得它可能跟MathType设置有关

hbghlyj

设两圆第二个交点为E，这就相当于顺相似三角形ABE,CDE的外心连线与AB+CD的比值$\geq\frac14$
将$\triangle$CDE以E为中心旋转,由于有两个转向,不妨设C落在AB延长线上时PQ最小,如果这旋转过程中某一时刻使BCD共线,就交换$\triangle$ABE,CDE的地位,总之,能达到这个相对位置而使旋转过程中四边形ABCD总是凸的.
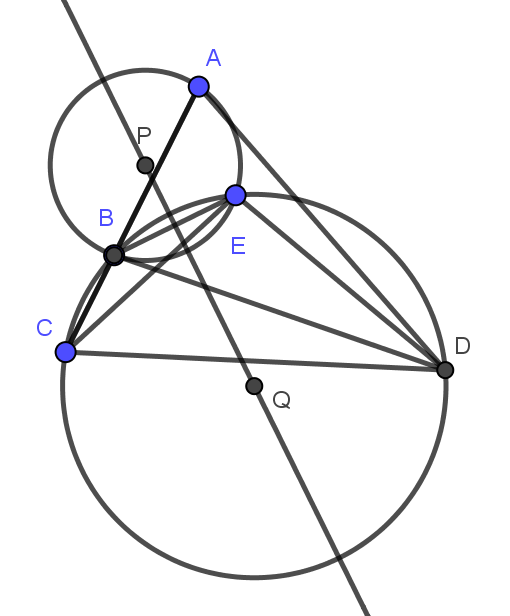
C在AB延长线上运动时,$\triangle PEQ\sim\triangle AEC,\angle EPQ=\angle CAE$,可见Q在过P的直线上运动,设线段PQ与$\odot P,\odot Q$交于G,H,则$2PQ\ge PG+HQ=PE+EQ$,所以$2PQ\ge PE+EQ$,又$PE\ge \frac{AB}2$,所以$\frac{PQ}{AB+CD}=\frac{PE}{AB}\frac{PQ}{PE+EQ}\ge\frac14$

hbghlyj

开始研究内心连线。。可ABO,ABE的内心不同，不能沿用8#的做法了。