|
|
Last edited by hbghlyj 2020-1-20 18:22
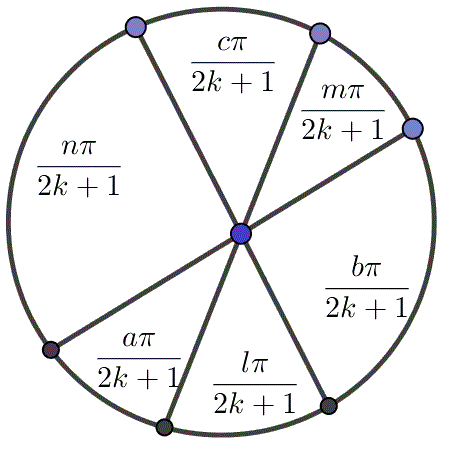
设三条对角线将圆周分成的六段弧分别对a,b,c,l,m,n条边,由三弦共点定理,它们的圆周角满足
是否存在$a,b,c,l,m,n,k\in\mathbf N_+$,a+b+c+l+m+n=2k+1,$\sin\frac{\pi a}{2k+1}\sin\frac{\pi b}{2k+1}\sin\frac{\pi c}{2k+1}=\sin\frac{\pi l}{2k+1}\sin\frac{\pi m}{2k+1}\sin\frac{\pi n}{2k+1}$,$(e^{\frac{\pi ai}{2k+1}}-e^{-\frac{\pi ai}{2k+1}})(e^{\frac{\pi bi}{k+1}}-e^{-\frac{\pi bi}{2k+1}})(e^{\frac{\pi ci}{2k+1}}-e^{-\frac{\pi ci}{2k+1}})=(e^{\frac{\pi li}{2k+1}}-e^{-\frac{\pi li}{2k+1}})(e^{\frac{\pi mi}{2k+1}}-e^{-\frac{\pi mi}{2k+1}})(e^{\frac{\pi ni}{2k+1}}-e^{-\frac{\pi ni}{2k+1}})$,设$A = {e^{\frac{{\pi ia}}{{2k + 1}}}},B=\cdots$,条件化为ABCLMN=1，
\[2 A B C+L M N (A^2 + B^2 + C^2) +
A B C (L^2 M^2 + L^2 N^2 + M^2 N^2)=2 L M N+A B C (L^2 + M^2 + N^2) + L M N(A^2 B^2 + A^2 C^2 +
B^2 C^2) \]然后怎么办,虽然形式很对称，却不能因式分解,消去n也无用 我只能破坏这个对称的形式了
把n消去，把a解出来\[a^2=\frac{b^2 c^2 l^2 m^2-b^2 l^2 m^2-c^2 l^2 m^2+2 l^2 m^2-l^2-m^2+1}{l^2 m^2 \left(b^2 c^2 l^2 m^2-b^2 c^2 l^2-b^2 c^2 m^2+2 b^2 c^2-b^2-c^2+1\right)}=1 + \frac{{ - 1 + \frac{1}{{{b^2}{c^2}{l^2}{m^2}}}}}{{1 + \frac{{\left( {1 - \frac{1}{{{b^2}}}} \right)\left( {1 - \frac{1}{{{c^2}}}} \right)}}{{\left( {1 - {l^2}} \right)\left( {1 - {m^2}} \right)}}}}\] |
|
