平面向量一题，求最值

realnumber

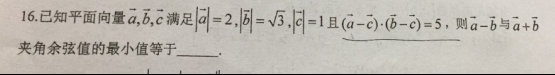
这样对吗？对的话，有没更简单办法
设$\vv{a}=(2\cos α,2\sin α),\vv{b}=(\sqrt{3}\cos β,\sqrt{3}\sin β),\vv{c}=(1,0)$
即求$\abs{\vv{a}-\vv{b}}\abs{\vv{a}+\vv{b}}=\sqrt{49-48\cos ^2 (α-β)}$的最大值.---(*)
而由$5=(\vv{a}-\vv{c})·(\vv{b}-\vv{c})$得到$2\sqrt{3}\cos (α-β)-4=2\cos α+\sqrt{3}\cos β \in [-\sqrt{7},\sqrt{7}]$把这个结果代入(*)

走走看看

回复 1# realnumber

\begin{align*}
cos<\vv{a}-\vv{b},\vv{a}+\vv{b}>&=\frac{a^2-b^2}{\sqrt{\vv{a}^2-2\vv{a}·\vv{b}+\vv{b}^2}\sqrt{\vv{a}^2+2\vv{a}·\vv{b}+\vv{b}^2}}\\
&=\frac{1}{\sqrt{49-4(\vv{a}\vv{b})^2}}  (*)\\
由已知得：
\vv{a}\vv{b}&=(\vv{a}+\vv{b})\vv{c}-\vv{c}^2+5\\
即\vv{a}\vv{b}&=(\vv{a}+\vv{b})\vv{c}+4\\
&≥-|\vv{a}+\vv{b}|+4\\
解得：
&1≤\vv{a}\vv{b}≤9\\
代入（*）得  &
cos<\vv{a}-\vv{b},\vv{a}+\vv{b}>≥\frac{1}{\sqrt{45}}=\frac{\sqrt{5}}{15}
\end{align*}