来自人教群：椭圆四边形两平分线外接圆最小

kuing

鄂***yuzi 2020/3/12 22:13:54
10．过点 $P(2,1)$ 斜率为正的直线交椭圆 $\frac{x^2}{24}+\frac{y^2}{5}=1$ 于 $A, B$ 两点．$C, D$ 是椭圆上相异的两点，满足 $C P, D P$ 分别平分 $\angle A C B, \angle A D B$ ．则 $\triangle P C D$ 外接圆半径的最小值为（）．
A．$\frac{2 \sqrt{15}}{5}$
B．$\frac{\sqrt{65}}{5}$
C．$\frac{24}{13}$
D．$\frac{19}{13}$

这个题摸不着头脑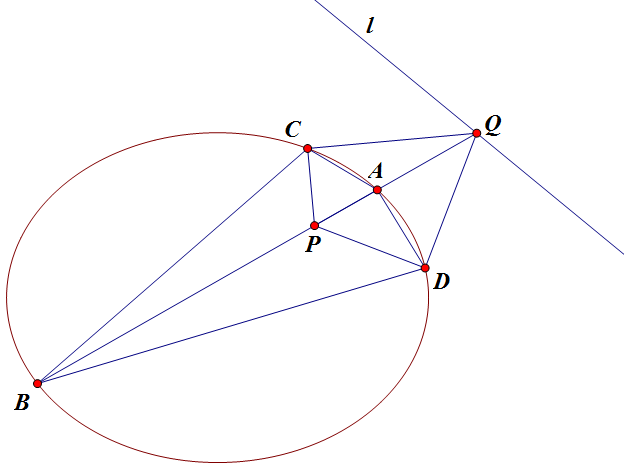

如图，设 `P` 关于椭圆的极线为 `l`，`AB` 交 `l` 于 `Q`，则 `B`, `P`, `A`, `Q` 调和，于是由 `CP` 是 `\angle ACB` 的平分线可知 `CQ` 是其外角平分线，亦即 `CP\perp CQ`，同理 `DP\perp DQ`，所以 `C`, `P`, `D`, `Q` 四点共圆且 `PQ` 就是直径，所以其最小值就是当 `PQ\perp l` 时，亦即 `2R\geqslant P` 到 `l` 的距离。

回到原题，极线 `l` 就是 `2x/24+y/5=1`，即 `5x+12y-60=0`，所以
\[
R_{\min}=\frac{\abs{10+12-60}}{2\sqrt{5^2+12^2}}=\frac{19}{13},
\]选 D。

isee

哇，极点极线的绝佳例子

kuing

讨论组 2020-03-13：
goft 10:14:56
我发个学生做的


第二个应该是老师做的吧

kuing

阿氏圆的解法也是很不错嘀，计算量也不大，更重要的是接地气些，相对来说极点极线调和啥的就有点高级了。

isee

回复 6# kuing


    阿氏圆就是调和点列最典型的“实例”