圆锥曲线中，两直线的关系

lemondian

如图，已知$A,B,C,D$为曲线$ax^2+by^2=1$上的四点，直线$AC,BD$相交于点$P(m,n)$.。
（1）若直线$AB$的方程为$Ax+By+C=0$,求直线$CD$的方程；
（2）若直线$AB$过定点$(x_0,y_0)$，证明直线$CD$也过定点，并求出定点的坐标；
（3）若直线$AB$过定点$(x_0,y_0)$，且其斜率为$k$，设直线$CD$的斜率为$k_2$，试求$k$与$k_2$的关系式。

kuing

（1）`P` 的极线 `l_P`: `amx+bny=1`，将其与 `AB` 联立解得
\[\left(\frac{B+b C n}{a B m-A b n},-\frac{A+a C m}{a B m-A b n}\right),\]该点亦是 `AB` 与 `CD` 的交点。

另一方面，过 `P` 且与 `l_P` 平行的直线为 `amx+bny=am^2+bn^2`，将其与 `AB` 联立解得
\[\left(\frac{B(am^2+bn^2)+b C n}{a B m-A b n},-\frac{A(am^2+bn^2)+a C m}{a B m-A b n}\right),\]则该点关于 `P` 的对称点在 `CD` 上。

综上，`CD` 过以下两点
\[\left(\frac{B+b C n}{a B m-A b n},-\frac{A+a C m}{a B m-A b n}\right),\left(2m-\frac{B(am^2+bn^2)+b C n}{a B m-A b n},2n+\frac{A(am^2+bn^2)+a C m}{a B m-A b n}\right),\]然后用两点式啥的，化简后最终结果是
\[(a m^2 + b n^2 - 1) (A x + B y + C) = 2 (A m + B n + C) (a m x + b n y - 1).\]
（结果这么简洁，肯定有更简单方法……

kuing

（2）题意是假设 `P` 是定点？那样的话，`CD` 过定点的结论就和上次这帖是一样道理，即：设过 `(x_0,y_0)` 和 `P` 的直线交 `l_P` 于 `Q`，交 `CD` 于 `R`，则 `(x_0,y_0)`, `P`, `R`, `Q` 调和，从而 `R` 为定点，根据调和即可算出具体坐标。
另外说一下，假如恰好 `(x_0,y_0)` 是 `PQ` 中点，那么 `R` 就变成无穷远点，此时 `CD` 就不是过定点，而是斜率恒定，所以其实原结论存在瑕疵。

至于斜率关系，上次那帖的定点都在 `x` 轴上所以结论简单，这回恐怕会麻烦得多，当然用楼上的结果强算应该能算出来，但我不想撸了……

kuing

回复 2# kuing

再把（1）撸一遍（其实就是由结果反推得出的所谓过程



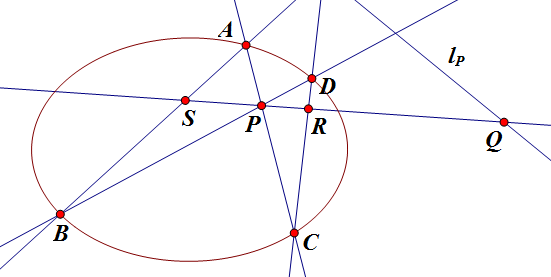
如上图，过 `P` 任作一直线交其极线 `l_P` 于 `Q`，交 `AB`, `CD` 于 `S`, `R`，则 `S`, `P`, `R`, `Q` 调和，于是有
\[
\frac1{\overline{RQ}}+\frac1{\overline{SQ}}=\frac2{\overline{PQ}}\riff\frac{2\overline{RQ}}{\overline{PQ}}=1+\frac{\overline{RQ}}{\overline{SQ}}=1+\frac{\overline{PR}}{\overline{SP}}=\frac{\overline{SR}}{\overline{SP}},
\]（均为有向线段，下同）设 `R(x,y)`，那么
\begin{align*}
\frac{\overline{RQ}}{\overline{PQ}}&=\frac{amx+bny-1}{am^2+bn^2-1},\\
\frac{\overline{SR}}{\overline{SP}}&=\frac{Ax+By+C}{Am+Bn+C},
\end{align*}从而 `CD` 的方程就是
\[2\cdot\frac{amx+bny-1}{am^2+bn^2-1}=\frac{Ax+By+C}{Am+Bn+C},\]也就是 2# 的结果。