|
|
original poster
hbghlyj
posted 2020-4-26 10:22
Last edited by hbghlyj 2020-4-26 14:50S是圆的集合,S中的任意圆对的根轴都是ε,则S称为"共轴圆束"或"共轴圆组"
第一种.双曲线型.S是经过A,B的圆的集合,ε是直线AB.S中所有圆的中心的集合是线段AB的中垂线,称为S的"中心线".S中最小的圆是以AB为直径的圆,S中没有最大的圆,当半径增大时,两侧的圆都趋于ε,将其视为S的退化元素,半径为∞.
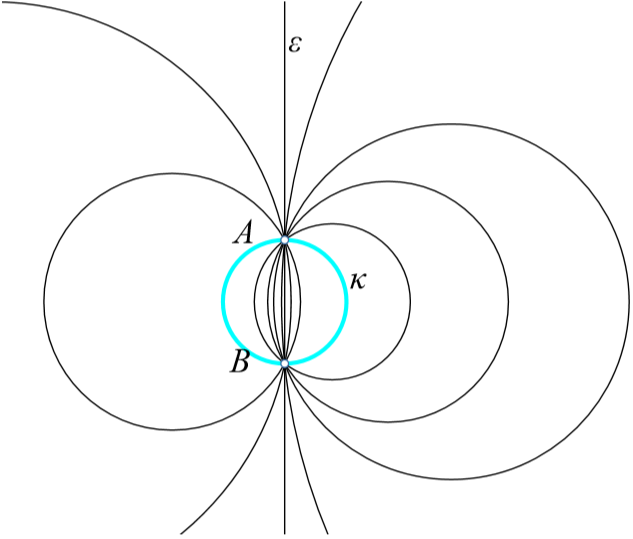
第二种.椭圆型.S中的圆没有公共点.S是线段AB的阿氏圆的集合.根据定义,S中一个圆κ满足X∈κ⇔XA/XB=k,k是常数。ε是线段AB的中垂线,“中心线”是直线AB.点A,B称为S的“极限点”,将其视为S的退化元素,半径为0.S中没有最大的圆,当半径增大时,两侧的圆都趋于ε,将其视为S的退化元素,半径为∞.
可以用下面的定理来判定C中的圆κ:
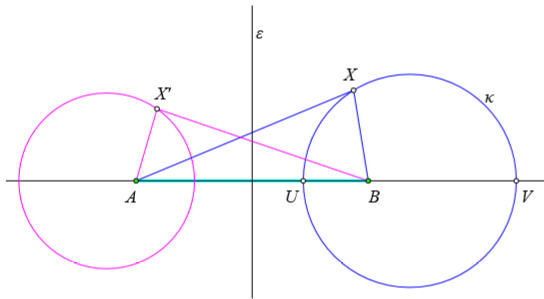
定理1.椭圆型圆束的极限点A,B关于C的每个圆κ对称,它们也关于κ与中心线的交点U,V调和共轭。反过来,以每一对AB的调和分割点为直径作的圆在C中。
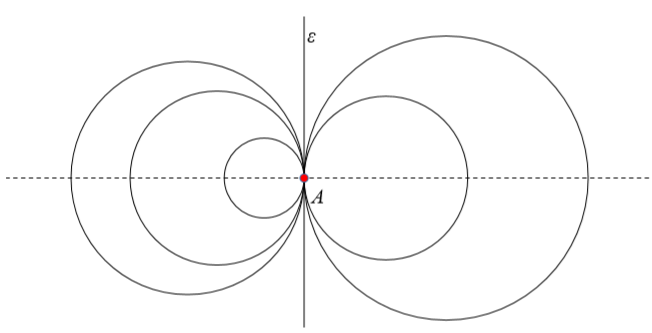
第三种.抛物线型.在前两种圆束中,当A,B重合时,S是与ε相切于A的所有圆的集合.此时最小的圆的半径为0.
|
|